题目内容

函数f₁（x）=cosx-sinx，记f₂（x）=f₁′（x），f₃（x）=f₂′（x），…f_n（x）=f_n-1′（x），（n∈N^*，n≥2），则 $数学公式$ =

A.
$数学公式$
B.
$数学公式$
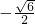
C.
0
D.
2008

B
分析：先求出f₂（x）、f₃（x）、f₄（x），观察所求的结果，归纳其中的周期性规律，求解即可．
解答：由题意，f₂（x）=f₁′（x）=-sinx-cosx
f₃（x）=f₂′（x）=-cosx+sinx，
f₄（x）=（-cosx+sinx）′=sinx+cosx，
f₅（x）=cosx-sinx，
以此类推，可得出f_n（x）=f_n+4（x）
又∵f₁（x）+f₂（x）+f₃（x）+f₄（x）=0，
∴ $\text{[math]}$ = $\text{[math]}$ =- $\text{[math]}$ ．
故选B．
点评：本题以三角函数为载体，考查三角函数的导数、周期性、及观察归纳思想的运用，解题的关键是判断出函数导数变化的周期性．．

练习册系列答案

一诺书业寒假作业快乐假期系列答案

开心寒假作业年度复习方案系列答案

阳光试卷中考总复习试卷系列答案

海淀黄冈名师期末冲刺系列答案

久为教育期末真题汇编精选卷系列答案

中考全优复习策略系列答案

昕金立文化中考一本全系列答案

模拟试卷汇编优化系列答案

学期总复习期末复习寒假作业系列答案

赢在课堂中考先锋总复习卷系列答案

相关题目

，5]，其中m是不等于零的常数，
（1）（理）写出h（4x）的定义域；
（文）m=1时，直接写出h（x）的值域；
（2）（文、理）求h（x）的单调递增区间；
（3）已知函数f（x）（x∈[a，b]），定义：f₁（x）=minf（t）|a≤t≤x（x∈[a，b]），f₂（x）=maxf（t）|a≤t≤x（x∈[a，b]）．其中，minf（x）|x∈D表示函数f（x）在D上的最小值，maxf（x）|x∈D表示函数f（x）在D上的最大值．例如：f（x）=cosx，x∈[0，π]，则f₁（x）=cosx，x∈[0，π]，f₂（x）=1，x∈[0，π]．
（理）当m=1时，设M(x)=

，不等式t≤M₁（x）-M₂（x）≤n恒成立，求t，n的取值范围；
（文）当m=1时，|h₁（x）-h₂（x）|≤n恒成立，求n的取值范围．

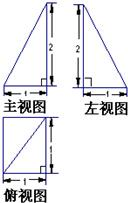（理）设6张卡片上分别写有函数f₁（x）=x、f₂（x）=x²、f₃（x）=x³、f₄（x）=sinx、f₅（x）=cosx和f₆（x）=lg（|x|+1）．
（Ⅰ）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数
的概率；
（Ⅱ）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片，则停止抽取，否则继续进行，求抽取次数ξ的分布列和数学期望．
（文）已知四棱锥P-ABCD的三视图如下图所示，E是侧棱PC上的动点．
（Ⅰ）求四棱锥P-ABCD的体积；
（Ⅱ）是否不论点E在何位置，都有BD⊥AE？证明你的结论．

（2009•浦东新区一模）对于函数f₁（x），f₂（x），h（x），如果存在实数a，b使得h（x）=a•f₁（x）+b•f₂（x），那么称h（x）为f₁（x），f₂（x）的生成函数．
（1）下面给出两组函数，h（x）是否分别为f₁（x），f₂（x）的生成函数？并说明理由．
第一组：f1(x)=sinx，f2(x)=cosx，h(x)=sin(x+

)；
第二组：f₁（x）=x²-x，f₂（x）=x²+x+1，h（x）=x²-x+1．
（2）设f1(x)=log2x，f2(x)=log

x，a=2，b=1，生成函数h（x）．若不等式h（4x）+t•h（2x）＜0在x∈[2，4]上有解，求实数t的取值范围．
（3）设f1(x)=x(x＞0)，f2(x)=

(x＞0)，取a＞0，b＞0生成函数h（x）图象的最低点坐标为（2，8）．若对于任意正实数x₁，x₂且x₁+x₂=1，试问是否存在最大的常数m，使h（x₁）h（x₂）≥m恒成立？如果存在，求出这个m的值；如果不存在，请说明理由．

函数f₁（x）=cosx-sinx，记f₂（x）=f₁′（x），f₃（x）=f₂′（x），…f_n（x）=f_n-1′（x），（n∈N^*，n≥2），则f1(