题目内容
若数列{an}满足:a1=19, ,则数列{an}的前n项和数值最大时,n的值是
,则数列{an}的前n项和数值最大时,n的值是
- A.6
- B.7
- C.8
- D.9
B
分析:先由题设条件求出an=19+(n-1)×(-3)=22-3n,再由an=22-3n≥0,得n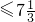 ,由此得到数列{an}的前n项和数值最大时,n的值.
,由此得到数列{an}的前n项和数值最大时,n的值.
解答:∵a1=19, ,
,
∴数列{an}是首项为19,公差为-3的等差数列,
∴an=19+(n-1)×(-3)=22-3n,
由an=22-3n≥0,得n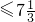 ,
,
∴数列{an}的前n项和数值最大时,n的值是7.
故选B.
点评:本题考查等差数列的性质和应用,是基础题.解题时要认真审题,仔细解答.
分析:先由题设条件求出an=19+(n-1)×(-3)=22-3n,再由an=22-3n≥0,得n
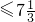 ,由此得到数列{an}的前n项和数值最大时,n的值.
,由此得到数列{an}的前n项和数值最大时,n的值.解答:∵a1=19,
 ,
,∴数列{an}是首项为19,公差为-3的等差数列,
∴an=19+(n-1)×(-3)=22-3n,
由an=22-3n≥0,得n
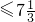 ,
,∴数列{an}的前n项和数值最大时,n的值是7.
故选B.
点评:本题考查等差数列的性质和应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目