题目内容
如图,在直三棱柱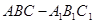 中,
中,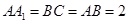 ,
,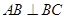 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。
(1)求二面角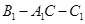 的大小。
的大小。
(2)证明:在AB上存在一个点Q,使得平面 ⊥平面
⊥平面 ,
,
并求出 的长度。
的长度。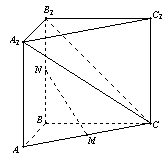
(1) ;(2)详见解析
;(2)详见解析
解析试题分析:(1)有两种思路,其一是利用几何体中的垂直关系,以B为坐标原点, 所在的直线分别为,
所在的直线分别为, 轴,
轴, 轴,
轴, 轴建立空间直角坐标系,利用平面
轴建立空间直角坐标系,利用平面 与平面
与平面 的法向量的夹角求二面角的大小.其二是按照作出二面角的平面角,并在三角形中求出该角的方法,利用平面
的法向量的夹角求二面角的大小.其二是按照作出二面角的平面角,并在三角形中求出该角的方法,利用平面 平面
平面 ,在平面
,在平面 内过点
内过点 作
作 ,垂足是
,垂足是 ,过作
,过作 ,垂足为
,垂足为 ,连结
,连结 ,得二面角
,得二面角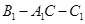 的平面角
的平面角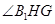 ,最后在直角三角形
,最后在直角三角形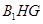 中求
中求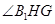 ;
;
(2)在空间直角坐标系中,设 ,求出平面
,求出平面 的法向量
的法向量 ,和平面
,和平面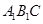 的法向量
的法向量
再由 确定点
确定点 的坐标,进而求线段
的坐标,进而求线段 的长度.
的长度.
方法一(向量法):如图建立空间直角坐标系 1分
(1)

设平面 的法向量为
的法向量为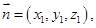 ,平面
,平面 的法向量为
的法向量为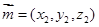
则有 3分
3分 5分
5分
设二面角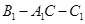 为
为 ,则
,则 
∴二面角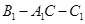 的大小为60°。 6分
的大小为60°。 6分
(2)设 , ∵
, ∵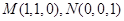
∴ ,设平面
,设平面 的法向量为
的法向量为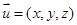
则有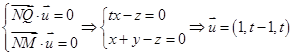 10分
10分
由(1)可知平面 的法向量为
的法向量为 ,
, 平面
平面 平面
平面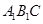
 即
即 此时
此时 ,
,

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
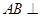 侧面
侧面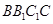 ,AB=BC=1,BB1=2,∠BCC1=
,AB=BC=1,BB1=2,∠BCC1= .
.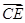 =l
=l (0≤l≤1),且平面AB1E与BB1E所成的锐二面角
(0≤l≤1),且平面AB1E与BB1E所成的锐二面角 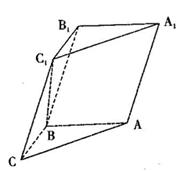
 是正方形,
是正方形, 平面
平面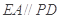 ,
,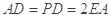 ,
,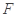 ,
, ,
, 分别为
分别为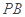 ,
,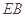 ,
,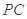 的中点.
的中点.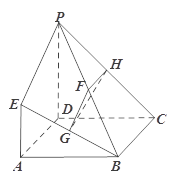
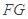
 平面
平面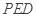 ;
;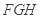 与平面
与平面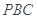 所成锐二面角的大小.
所成锐二面角的大小.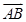 ,
,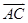 为边的平行四边形的面积;
为边的平行四边形的面积;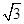 ,且a分别与
,且a分别与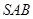 所在平面与直角梯形
所在平面与直角梯形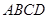 所在平面垂直,且
所在平面垂直,且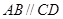 ,
,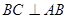 ,
,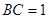 ,
,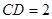 ,
, 、
、 分别是线段
分别是线段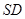 、
、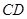 的中点.
的中点.
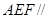 平面
平面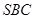 ;
;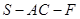 的余弦值.
的余弦值.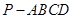 的底面为正方形,侧面
的底面为正方形,侧面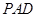
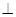 底面
底面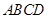 .
.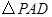 为等腰直角三角形,且
为等腰直角三角形,且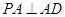 .
. ,
,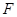 分别为底边
分别为底边 和侧棱
和侧棱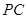 的中点.
的中点.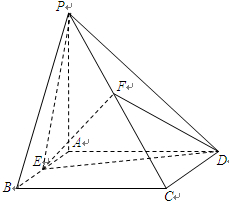
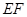 ∥平面
∥平面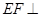 平面
平面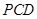 ;
; 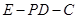 的余弦值.
的余弦值. 的棱长为1,点
的棱长为1,点 在侧面
在侧面 及其边界上运动,并且总保持
及其边界上运动,并且总保持 平行平面
平行平面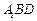 ,则动点P的轨迹的长度是 _______ .
,则动点P的轨迹的长度是 _______ .

 ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.