题目内容
已知数列{an}的前n项和为Sn,函数![]() (其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N*)均在函数
(其中p、q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(n,2Sn)(n∈N*)均在函数![]() 的图象上(其中是
的图象上(其中是![]() 函数f(x)的导函数).
函数f(x)的导函数).
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)记bn=an·qn,求数列{bn}的前n项和Tn.
答案:
解析:
解析:
|
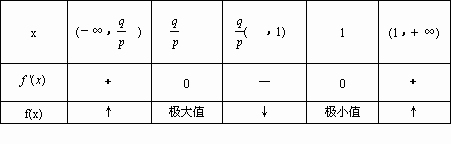
(1) 令
由上表可知,x=1时,f(x)取得极小值,因此a1=1. (2) ∵点(n,2Sn)(n∈N*)均在函数 由于a1=1,所以2a1=2p,得p=1,∴ 上面两式相减,得 (3)由 由题设p>q>0,而p=1,故q≠1, |

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |