题目内容
用数学归纳法说明:1+ ,在第二步证明从n=k到n=k+1成立时,左边增加的项数是________项.
,在第二步证明从n=k到n=k+1成立时,左边增加的项数是________项.
2k
分析:当n=k成立, +
+ +…+
+…+ <k,当n=k+1时,写出对应的关系式,观察计算即可.
<k,当n=k+1时,写出对应的关系式,观察计算即可.
解答:在用数学归纳法证明:1+ ,在第二步证明时,
,在第二步证明时,
假设n=k时成立,即 +
+ +…+
+…+ <k,
<k,
则n=k+1成立时,有 +
+ +…+
+…+ +
+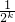 +…+
+…+ <k+1,
<k+1,
∴左边增加的项数是(2k+2k-1)-(2k-1)=2k.
故答案为:2k.
点评:本题考查数学归纳法,考查n=k到n=k+1成立时左边项数的变化情况,考查理解与应用的能力,属于中档题.
分析:当n=k成立,
 +
+ +…+
+…+ <k,当n=k+1时,写出对应的关系式,观察计算即可.
<k,当n=k+1时,写出对应的关系式,观察计算即可.解答:在用数学归纳法证明:1+
 ,在第二步证明时,
,在第二步证明时,假设n=k时成立,即
 +
+ +…+
+…+ <k,
<k,则n=k+1成立时,有
 +
+ +…+
+…+ +
+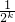 +…+
+…+ <k+1,
<k+1,∴左边增加的项数是(2k+2k-1)-(2k-1)=2k.
故答案为:2k.
点评:本题考查数学归纳法,考查n=k到n=k+1成立时左边项数的变化情况,考查理解与应用的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,在第二步证明从n=k到n=k+1成立时,左边增加的项数是 项.
,在第二步证明从n=k到n=k+1成立时,左边增加的项数是 项.