题目内容

设抛物线y2=2px(p＞0)的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴.证明直线AC经过原点O.

思路分析：本题若设直线AB的点斜式方程也可以,但必须要讨论斜率k不存在的情况,另外,证明直线AC过原点O,这里是利用了直线OC与直线AC斜率相等,非常简捷,如若写出直线AC的方程,通过(0,0)适合方程来证明将较复杂.

证明:∵抛物线的焦点为F(,0),∴经过点F的直线AB的方程可设为x=my+,

代入抛物线方程,得y2-2pmy-p2=0.

设A(x1,y1),B(x2,y2),则y1、y2是该方程的两根,∴y1y2=-p2.

∵BC∥x轴,且点C在准线x=上,∴点C的坐标为(,y2).

∴直线OC的斜率为k=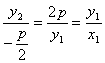,即k也是直线OA的斜率.

∴直线AC经过原点O.

练习册系列答案
相关题目
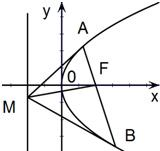精英家教网设抛物线y2=2px（p＞0）的焦点为F，经过点F的直线交抛物线于A，B两点，且A，B两点坐标分别为（x1，y1）、（x2，y2），y1＞0，y2＜0，M是抛物线的准线上的一点，O是坐标原点．若直线MA，MF，MB的斜率分别记为：KMA=a，KMF=b，KMB=c，（如图）
（I）若y1y2=-4，求抛物线的方程；
（II）当b=2时，求a+c的值；
（III）如果取KMA=2，KMB=-
12
时，判定|∠AMF-∠BMF|和∠MFO的值大小关系．并说明理由．
7、设抛物线y2=2px（p＞0）上一点A（1，2）到点B（x0，0）的距离等于到直线x=-1的距离，则实数x0的值是
1
．
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上．设抛物线y2=2px（p＞0），弦AB过焦点，△ABQ为阿基米德三角形，则△ABQ为（　　）
设抛物线y2=2px（p＞0）的焦点为F，其准线与x轴的交点为Q，过Q点的直线l交抛物线于A，B两点．
（1）若直线l的斜率为
2
2
，求证：
FA
•
FB
=0；
（2）设直线FA，FB的斜率分别为k1，k2，求k1+k2的值．
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上．设抛物线y2=2px（p＞0），弦AB过焦点，△ABQ为其阿基米德三角形，则△ABQ的面积的最小值为（　　）
A、
p2
2
B、p2
C、2p2
D、4p2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网