题目内容
函数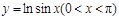 的大致图象是 ( )
的大致图象是 ( )
A. B. C. D.
C
解析试题分析:因为 时,
时, ,且正弦函数的图象先升后降,由复合函数的单调性知,
,且正弦函数的图象先升后降,由复合函数的单调性知,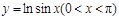 的图象应是先升后降,故选C。
的图象应是先升后降,故选C。
考点:对数函数、正弦函数的图象,复合函数的单调性。
点评:简单题,通过研究复合函数的单调性等,明确函数图象的大致形态。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
函数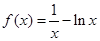 的零点个数为( )
的零点个数为( )
A. | B. | C.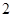 | D.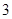 |
已知y=f(x)是奇函数,当x>0时,f(x)=2x(1-x),当x<0时f(x)应该等于 ( )
| A.–2x(1-x) | B.2x(1-x) | C.–2x(1+x) | D.2x(1+x) |
下列函数中,定义域为[0,∞)的函数是 ( )
A.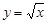 | B.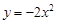 | C.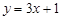 | D.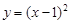 |
 是以
是以 为周期的奇函数,若
为周期的奇函数,若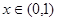 时,
时, ,则
,则 在区间
在区间 上是( )
上是( )
A.增函数且 | B.减函数且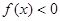 |
C.增函数且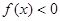 | D.减函数且 |
已知下列不等式: ,则在
,则在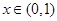 内上述不等式恒成立的个数为( )
内上述不等式恒成立的个数为( )
| A.1 | B.2 | C.3 | D.4 |
已知函数 ,若实数
,若实数 是函数
是函数 的零点,且
的零点,且 ,则
,则 的值为 ( )
的值为 ( )
| A.恒为正值 | B.等于0 | C.恒为负值 | D.不大于0 |
函数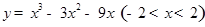 有 ( )
有 ( )
A.最大值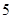 ,最小值-22 ,最小值-22 | B.最大值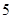 ,最小值-2 ,最小值-2 |
C.最大值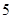 ,无最小值 ,无最小值 | D.最小值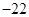 ,无最大值 ,无最大值 |
 的定义域为 ( )
的定义域为 ( )