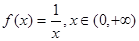题目内容
下列函数中,反函数是其自身的函数为( )
| A、f(x)=x3,x∈[0,+∞) | ||
| B、f(x)=x3,x∈[-∞,+∞) | ||
| C、f(x)=cx,x∈(-∞,+∞) | ||
D、f(x)=
|
分析:求出各个选项中函数的反函数,考查反函数是否是它本身,从而选出答案.
解答:解:∵f(x)=x3,x∈[0,+∞)的反函数是 y=
,x∈[0,+∞),故A不满足条件.
∵f(x)=x3,x∈(-∞,+∞)的反函数是 y=
,x∈(-∞,+∞),故B不满足条件.
∵f(x)=cx,x∈(-∞,+∞)的反函数是 y=logcx,x>0,故C不满足条件.
∵f(x)=
,x∈(0,+∞)的反函数是f-1(x)=
,x∈(0,+∞),和原函数相同,故D满足条件.
综上,只有D满足条件,
故选D.
| 3 | x |
∵f(x)=x3,x∈(-∞,+∞)的反函数是 y=
| 3 | x |
∵f(x)=cx,x∈(-∞,+∞)的反函数是 y=logcx,x>0,故C不满足条件.
∵f(x)=
| 1 |
| x |
| 1 |
| x |
综上,只有D满足条件,
故选D.
点评:本题考查球翻书的方法,注意反函数的定义域是原函数的值域.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
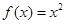 ,
,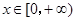 B.
B.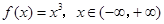
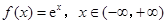 D.
D.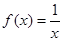 ,
,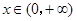
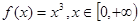 (B)
(B)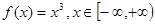
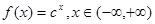 (D)
(D)