题目内容
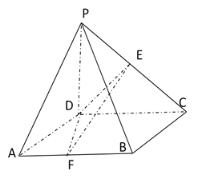
【题目】如图,扇形![]() 的半径为
的半径为![]() ,圆心角
,圆心角![]() ,点
,点![]() 为弧
为弧![]() 上一点,
上一点,![]() 平面
平面![]() 且
且![]() ,点
,点![]() 且
且![]() ,
,![]() ∥平面
∥平面![]() .
.
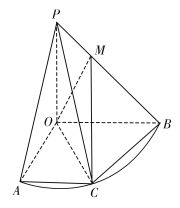
(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)求平面![]() 和平面
和平面![]() 所成二面角的正弦值的大小.
所成二面角的正弦值的大小.
【答案】(1)见证明;(2) ![]()
【解析】
(1)如图,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,结合
,结合![]() ∥平面
∥平面![]() ,得到
,得到![]() ∥
∥![]() ,从而求得
,从而求得![]() ,根据余弦定理得
,根据余弦定理得![]() ,得到
,得到![]() ,得到
,得到![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,得到
,得到![]() 平面
平面![]() ,再利用面面垂直的判定定理证得平面
,再利用面面垂直的判定定理证得平面![]()
![]() 平面
平面![]() ;
;
(2)由(1)的条件,得到![]() ,建立空间直角坐标系
,建立空间直角坐标系![]() ,得到点的坐标,求得面的法向量,用法向量所成角的余弦值得到二面角的余弦值,再应用同角三角函数关系式求得其正弦值,得到答案.
,得到点的坐标,求得面的法向量,用法向量所成角的余弦值得到二面角的余弦值,再应用同角三角函数关系式求得其正弦值,得到答案.
(1)如图,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
![]()
![]() ∥平面
∥平面![]() ,
,![]()
![]() ∥
∥![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 在
在![]() 中,根据余弦定理得
中,根据余弦定理得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
又![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
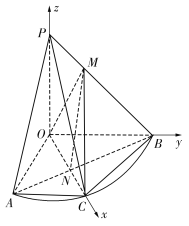
(2)由(1)得![]() ,如图建立空间直角坐标系
,如图建立空间直角坐标系![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 点
点![]() 且
且![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则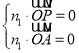 ,即
,即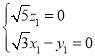 ,
,
令![]() ,得
,得![]() ,
,![]() ,
,![]()
![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则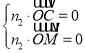 ,即
,即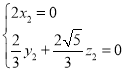 ,即
,即 ,令
,令![]() ,得
,得![]() ,
,![]() ,
,![]()
![]() ,
,
设平面![]() 和平面
和平面![]() 所成二面角的大小为
所成二面角的大小为![]() ,
,
则![]() ,
,![]() ,
,
∴平面![]() 和平面
和平面![]() 所成二面角的正弦值的大小为
所成二面角的正弦值的大小为![]()

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目