题目内容
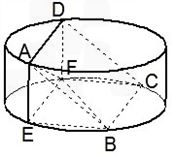
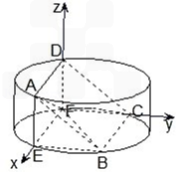
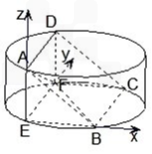
如图,圆柱的高为2,底面半径为3,AE、DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形.
(Ⅰ)求证:BC⊥BE;
(Ⅱ)求正方形ABCD的边长;
(Ⅲ)求直线EF与平面ABF所成角的正弦值.
(Ⅰ)求证:BC⊥BE;
(Ⅱ)求正方形ABCD的边长;
(Ⅲ)求直线EF与平面ABF所成角的正弦值.
解:(I)∵AE是圆柱的母线
∴AE⊥底面BEFC,
又BC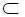 面BEFC∴AE⊥BC
面BEFC∴AE⊥BC
又∵ABCD是正方形∴AB⊥BC
又AE∩AB=A∴BC⊥面ABE
又BE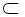 面ABE∴BC⊥BE
面ABE∴BC⊥BE
(II)∵四边形AEFD为矩形,且ABCD是正方形
∴EF BC
BC
∵BC⊥BE∴四边形EFBC为矩形
∴BF为圆柱下底面的直径
设正方形ABCD的边长为x,
则AD=EF=AB=x
在直角△AEB中AE=2,AB=x,且BE2+AE2=AB2,得BE2=x2﹣4
在直角△BEF中BF=6,EF=x,且BE2+EF2=BF2,的BE2=36﹣x2
解得x=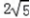 ,即正方形ABCD的边长为
,即正方形ABCD的边长为 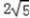
(III)解:如图以F为原点建立空间直角坐标系,
则A(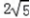 ,0,2),B(
,0,2),B(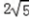 ,4,0),E(
,4,0),E(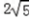 ,0,0),
,0,0), =(
=( 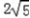 ,0,2),
,0,2),  =(
=( 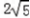 ,4,0),
,4,0),  =(
=(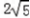 ,0,0)
,0,0)
设面AEF的法向量为 =(x,y,z),则
=(x,y,z),则 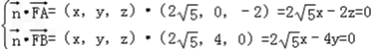
令x=1,则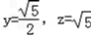 ,即
,即  =(1,
=(1,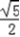 ,
,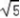 )
)
设直线EF与平面ABF所成角的大小为θ,
则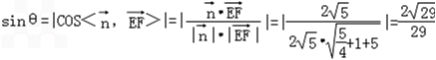
所以直线EF与平面ABF所成角的正弦值为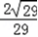 .
.
∴AE⊥底面BEFC,
又BC
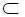 面BEFC∴AE⊥BC
面BEFC∴AE⊥BC又∵ABCD是正方形∴AB⊥BC
又AE∩AB=A∴BC⊥面ABE
又BE
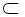 面ABE∴BC⊥BE
面ABE∴BC⊥BE(II)∵四边形AEFD为矩形,且ABCD是正方形
∴EF
 BC
BC ∵BC⊥BE∴四边形EFBC为矩形
∴BF为圆柱下底面的直径
设正方形ABCD的边长为x,
则AD=EF=AB=x
在直角△AEB中AE=2,AB=x,且BE2+AE2=AB2,得BE2=x2﹣4
在直角△BEF中BF=6,EF=x,且BE2+EF2=BF2,的BE2=36﹣x2
解得x=
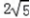 ,即正方形ABCD的边长为
,即正方形ABCD的边长为 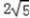
(III)解:如图以F为原点建立空间直角坐标系,
则A(
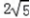 ,0,2),B(
,0,2),B(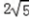 ,4,0),E(
,4,0),E(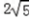 ,0,0),
,0,0), =(
=( 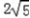 ,0,2),
,0,2),  =(
=( 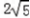 ,4,0),
,4,0), 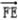 =(
=(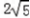 ,0,0)
,0,0)设面AEF的法向量为
 =(x,y,z),则
=(x,y,z),则 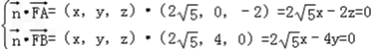
令x=1,则
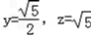 ,即
,即  =(1,
=(1,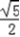 ,
,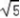 )
)设直线EF与平面ABF所成角的大小为θ,
则
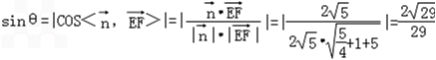
所以直线EF与平面ABF所成角的正弦值为
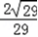 .
.


练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
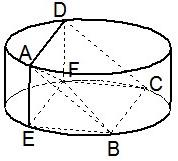 如图,圆柱的高为2,底面半径为3,AE、DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形.
如图,圆柱的高为2,底面半径为3,AE、DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形. ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 ;
; 与平面
与平面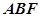 所成角的正弦值。
所成角的正弦值。
 ;
; 与平面
与平面 所成角的正弦值。
所成角的正弦值。