Question

（本小题满分12分）

如图，三棱锥P—ABC中， PC平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD平面PAB．

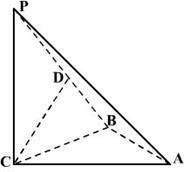(I) 求证：AB平面PCB；

(II) 求异面直线AP与BC所成角的大小；

（Ⅲ）求二面角C-PA-B的正弦值

Answer 1

（本小题满分12分）

解：(I) ∵PC平面ABC，平面ABC，∴PCAB．

∵CD平面PAB，平面PAB，∴CDAB．

又，∴AB平面PCB．

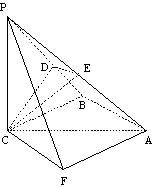
(II) 过点A作AF//BC，且AF=BC，连结PF，CF．

则为异面直线PA与BC所成的角．

由（Ⅰ）可得AB⊥BC，∴CFAF．

由三垂线定理，得PFAF．

则AF=CF=，PF=，

在中，  tan∠PAF==，

∴异面直线PA与BC所成的角为．

（III）取AP的中点E，连结CE、DE． ∵PC=AC=2，∴CE PA，CE=．

∵CD平面PAB，由三垂线定理的逆定理，得  DE PA．

∴为二面角C-PA-B的平面角．

由(I) AB平面PCB，又∵AB=BC，可求得BC=．

在中，PB=，．

    在中， sin∠CED=．

∴二面角C-PA-B大小的正弦值是．