题目内容
已知f（x）=|x2-2x|，a＜b＜c＜d且f（a）=f（b）=f（c）=f（d）则a+2b+2c+d=
- A.6
- B.8
- C.4
- D.5
A
分析：图解法：画出函数f（x）=|x2-2x|，的图象，根据图象分析a与d、b与c的和，结合图形的对称性，从而求出a+2b+2c+d的取值即可．
解答：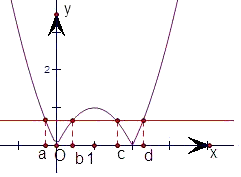
解：先画出函数f（x）=|x2-2x|的图象
∵a＜b＜c＜d且f（a）=f（b）=f（c）=f（d）
∴a与d、b与c都关于直线x=1的对称，
∴a+d=2．b+c=2，
则a+2b+2c+d=6
故选A．
点评：此题是中档题．考查利用函数图象分析解决问题的能力，以及绝对值函数图象的特点，体现数形结合的思想．
分析：图解法：画出函数f（x）=|x2-2x|，的图象，根据图象分析a与d、b与c的和，结合图形的对称性，从而求出a+2b+2c+d的取值即可．
解答：
解：先画出函数f（x）=|x2-2x|的图象∵a＜b＜c＜d且f（a）=f（b）=f（c）=f（d）
∴a与d、b与c都关于直线x=1的对称，
∴a+d=2．b+c=2，
则a+2b+2c+d=6
故选A．
点评：此题是中档题．考查利用函数图象分析解决问题的能力，以及绝对值函数图象的特点，体现数形结合的思想．
练习册系列答案
相关题目