题目内容
若函数f(x)在定义域上存在不相等的实数x1、x2,使得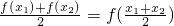 ,则称此函数为“和谐函数”.下列函数中是“和谐函数”的是
,则称此函数为“和谐函数”.下列函数中是“和谐函数”的是
- A.f(x)=x2
- B.f(x)=2x
- C.f(x)=tanx
- D.
C
分析:选项A可以用反证法;选项B和D可借助于图象直观说明;选项D取值验证即可.
解答:若f(x)=x2为和谐函数,则存在x1≠x2,使得 ,即
,即 ,所以有
,所以有 ,x1=x2,与x1≠x2矛盾,所以A不正确;
,x1=x2,与x1≠x2矛盾,所以A不正确;
等式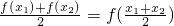 是指若点(x1,y1),(x2,y2)在一个函数图象上,它们的中点也在这个函数图象上,
是指若点(x1,y1),(x2,y2)在一个函数图象上,它们的中点也在这个函数图象上,
由指数函数f(x)=2x和对数函数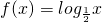 的图象如图可知,两函数图象上不存在两点满足上面等式,所以B、D不正确;
的图象如图可知,两函数图象上不存在两点满足上面等式,所以B、D不正确;
对于C,取 ,
, ,则有
,则有 ,所以函数f(x)=tanx为和谐函数.
,所以函数f(x)=tanx为和谐函数.
故选C.
点评:本题考查了进行简单的演绎推理,考查了反证法和特殊值法,考查了学生对指数函数和对数函数图的理解与掌握.
分析:选项A可以用反证法;选项B和D可借助于图象直观说明;选项D取值验证即可.
解答:若f(x)=x2为和谐函数,则存在x1≠x2,使得
 ,即
,即 ,所以有
,所以有 ,x1=x2,与x1≠x2矛盾,所以A不正确;
,x1=x2,与x1≠x2矛盾,所以A不正确;等式
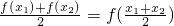 是指若点(x1,y1),(x2,y2)在一个函数图象上,它们的中点也在这个函数图象上,
是指若点(x1,y1),(x2,y2)在一个函数图象上,它们的中点也在这个函数图象上,
由指数函数f(x)=2x和对数函数
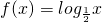 的图象如图可知,两函数图象上不存在两点满足上面等式,所以B、D不正确;
的图象如图可知,两函数图象上不存在两点满足上面等式,所以B、D不正确;对于C,取
 ,
, ,则有
,则有 ,所以函数f(x)=tanx为和谐函数.
,所以函数f(x)=tanx为和谐函数.故选C.
点评:本题考查了进行简单的演绎推理,考查了反证法和特殊值法,考查了学生对指数函数和对数函数图的理解与掌握.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目