题目内容
某工厂在试验阶段大量生产一种零件,这种零件有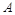 、
、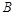 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为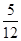 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为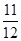 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽取该种零件4个,设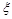 表示其中合格品的个数,求
表示其中合格品的个数,求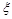 的分布列及数学期望
的分布列及数学期望 .
.
(1)一个零件经过检测为合格品的概率是 ;(2)分布列为
;(2)分布列为 ,其中
,其中 ,数学期望
,数学期望 .
.
解析试题分析:(1)设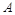 、
、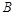 两项技术指标达标的概率分别为
两项技术指标达标的概率分别为 、
、 ,由题意可列方程解得
,由题意可列方程解得 、
、 ,所以一个零件经过检测为合格品的概率是
,所以一个零件经过检测为合格品的概率是 ;
;
(2)依题意知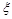 ~B(4,
~B(4, ),所以分布列为
),所以分布列为 ;数学期望为
;数学期望为 .
.
试题解析:(1)设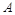 、
、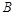 两项技术指标达标的概率分别为
两项技术指标达标的概率分别为 、
、
由题意,得 
解得  或
或 ,∴
,∴ .
.
即,一个零件经过检测为合格品的概率为 .
.
(2)依题意知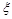 ~B(4,
~B(4, ),
),
分布列为 ,其中
,其中 ,
, .
.
考点:概率分布、数学期望与方差.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
(1)求
 ;
;(2)某医院计划采购一批该型号药品,从质量的稳定性角度考虑,你认为采购哪个药厂的产品
比较合适?
(3)检测单位从甲厂送检的样品中任取两份作进一步分析,在抽取的两份样品中,求至少有一份得分在(90,100]之间的概率.
 、
、 、
、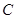 三道工序加工而成的,
三道工序加工而成的, 、
、 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场. 为三道加工工序中产品合格的工序数,求
为三道加工工序中产品合格的工序数,求 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.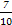 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少. ,
, ,
, ,现在3名工人独立地从中任意一个项目参与建设.
,现在3名工人独立地从中任意一个项目参与建设.