题目内容
如图,AB为⊙O的直径,点C,D在⊙O上,∠BAC=50°,则∠ADC= .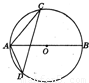
【答案】分析:利用圆的直径的性质、同圆中等弧所对的圆周角相等即可得出.
解答:解:连接BC,∵AB为⊙O的直径,∴∠ACB=90°.
又∠BAC=50°,∴∠ABC=90°-∠BAC=40°.
∵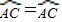 ,∴∠ADC=∠ABC=40°.
,∴∠ADC=∠ABC=40°.
故答案为40°.
点评:熟练掌握圆的直径的性质、同圆中等弧所对的圆周角相等是解题的关键.
解答:解:连接BC,∵AB为⊙O的直径,∴∠ACB=90°.
又∠BAC=50°,∴∠ABC=90°-∠BAC=40°.
∵
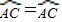 ,∴∠ADC=∠ABC=40°.
,∴∠ADC=∠ABC=40°.故答案为40°.
点评:熟练掌握圆的直径的性质、同圆中等弧所对的圆周角相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 .
. ;
; ;
; ,求
,求 的值.
的值.




 面体中有
面体中有 个面是直角三角形,则称这个
个面是直角三角形,则称这个 .那么四面体
.那么四面体 的直度为多少?说明理由;
的直度为多少?说明理由; (2)在四面体
(2)在四面体 ,设
,设 .若动点
.若动点 在四面体
在四面体 .设
.设 为动点
为动点 的函数,求
的函数,求 的正切值.
的正切值.