题目内容
已知函数 的定义域为A,函数g(x)=-3x+2,x∈[-1,1)的值域为B,求A∩B,A∪B,B∪CRA.
的定义域为A,函数g(x)=-3x+2,x∈[-1,1)的值域为B,求A∩B,A∪B,B∪CRA.
解:由已知得: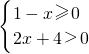
∴-2<x≤1
∴A=(-2,1]
∴CRA=(-∞,-2]∪(1,+∞)
又g(x)=-3x+2在[-1,1)上是减函数
∴B=(-1,5]
∴A∩B=(-1,1]
∴A∪B=(-2,5]
∴B∪CRA=(-∞,-2]∪(-1,+∞)
分析:根据分式的分母不为零且二次根式的被开方数大于或等于零,列式可以求出集合A,而根据一次函数的单调性可求出集合B,再根据集合的并、交和补集的含义,可得出答案.
点评:本题考查了函数的定义域和集合的交、并和补集等运算,属于基础题.兼顾分母和二次根式,准确求出函数的定义域即集合A,是解决本本题的关键.
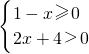
∴-2<x≤1
∴A=(-2,1]
∴CRA=(-∞,-2]∪(1,+∞)
又g(x)=-3x+2在[-1,1)上是减函数
∴B=(-1,5]
∴A∩B=(-1,1]
∴A∪B=(-2,5]
∴B∪CRA=(-∞,-2]∪(-1,+∞)
分析:根据分式的分母不为零且二次根式的被开方数大于或等于零,列式可以求出集合A,而根据一次函数的单调性可求出集合B,再根据集合的并、交和补集的含义,可得出答案.
点评:本题考查了函数的定义域和集合的交、并和补集等运算,属于基础题.兼顾分母和二次根式,准确求出函数的定义域即集合A,是解决本本题的关键.

练习册系列答案
相关题目
 的定义域为A,函数y=f[f(x)]的定义域为B,则( )
的定义域为A,函数y=f[f(x)]的定义域为B,则( ) 的定义域为[a,b],值域为[-2,1],则
的定义域为[a,b],值域为[-2,1],则 的值不可能是 ( )
的值不可能是 ( ) B.
B. C.
C. D.
D.
 的定义域为A,函数
的定义域为A,函数 的值域为B.
的值域为B. ;
; ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围. 的定义域为
的定义域为 B.
B.
 D.
D.