题目内容
椭圆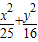 =1.点A(2,1),B(3,0),点P为椭圆上的动点.则|PA|+|PB|的最大值 .
=1.点A(2,1),B(3,0),点P为椭圆上的动点.则|PA|+|PB|的最大值 .
【答案】分析:根据椭圆的方程,算出它的焦点坐标为B(3,0)和B'(-3,0).因此连接PB'、AB',根据椭圆的定义得|PA|+|PB|=|PA|+(2a-|PB'|)=10+(|PA|-|PB'|).再由三角形两边之差小于第三边,得到当且仅当点P在AB'延长线上时,|PA|+|PB|=10+|AB'|=15达到最大值,从而得到本题答案.
解答: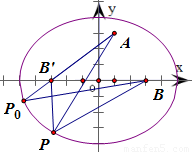 解:∵椭圆方程为
解:∵椭圆方程为 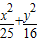 =1,
=1,
∴焦点坐标为B(3,0)和B'(-3,0)
连接PB'、AB',根据椭圆的定义,得|PB|+|PB'|=2a=10,可得|PB|=10-|PB'|
因此,|PA|+|PB|=|PA|+(10-|PB'|)=10+(|PA|-|PB'|)
∵|PA|-|PB'|≤|AB'|
∴|PA|+|PB|≤10+|AB'|=10+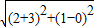 =10+
=10+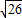 .
.
当且仅当点P在AB'延长线上时,等号成立
综上所述,可得|PA|+|PB|的最大值为10+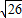
故答案为:10+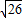 .
.
点评:本题给出椭圆内部一点A,求椭圆上动点P与A点和一个焦点距离B和的最大值,着重考查了椭圆的定义、标准方程和简单几何性质等知识,属于基础题.
解答:
 解:∵椭圆方程为
解:∵椭圆方程为 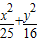 =1,
=1,∴焦点坐标为B(3,0)和B'(-3,0)
连接PB'、AB',根据椭圆的定义,得|PB|+|PB'|=2a=10,可得|PB|=10-|PB'|
因此,|PA|+|PB|=|PA|+(10-|PB'|)=10+(|PA|-|PB'|)
∵|PA|-|PB'|≤|AB'|
∴|PA|+|PB|≤10+|AB'|=10+
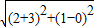 =10+
=10+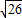 .
.当且仅当点P在AB'延长线上时,等号成立
综上所述,可得|PA|+|PB|的最大值为10+
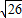
故答案为:10+
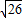 .
.点评:本题给出椭圆内部一点A,求椭圆上动点P与A点和一个焦点距离B和的最大值,着重考查了椭圆的定义、标准方程和简单几何性质等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率
已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率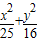 =1.点A(2,1),B(3,0),点P为椭圆上的动点.则|PA|+|PB|的最大值 .
=1.点A(2,1),B(3,0),点P为椭圆上的动点.则|PA|+|PB|的最大值 .