题目内容
已知函数f(x)=sin(π-ωx)cosωx+cos2ωx(ω>0)的最小正周期为π.(Ⅰ)求ω的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的
 ,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间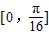 上的最小值.
上的最小值.
【答案】分析:(1)本小题主要考查综合运用三角函数公式、三角函数的性质,进行运算、变形、转换和求解的能力.
(2)要求三角函数的有关性质的问题,题目都要变形到y=Asin(ωx+φ)的形式,变形时利用诱导公式和二倍角公式逆用.
解答:解:(Ⅰ)∵f(x)=sin(π-ωx)cosωx+cos2ωx,
∴f(x)=sinωxcosωx+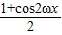
= sin2ωx+
sin2ωx+ cos2ωx+
cos2ωx+
=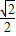 sin(2ωx+
sin(2ωx+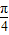 )+
)+
由于ω>0,依题意得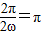 ,
,
所以ω=1;
(Ⅱ)由(Ⅰ)知f(x)=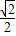 sin(2x+
sin(2x+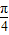 )+
)+ ,
,
∴g(x)=f(2x)=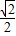 sin(4x+
sin(4x+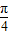 )+
)+
∵0≤x≤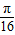 时,
时,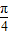 ≤4x+
≤4x+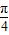 ≤
≤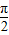 ,
,
∴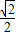 ≤sin(4x+
≤sin(4x+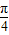 )≤1,
)≤1,
∴1≤g(x)≤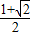 ,
,
g(x)在此区间内的最小值为1.
点评:利用同角三角函数间的关系式可以化简三角函数式(1)化简的标准:第一,尽量使函数种类最少,次数最低,而且尽量化成积的形式;第二,能求出值的要求出值;第三,根号内的三角函数式尽量开出.
(2)要求三角函数的有关性质的问题,题目都要变形到y=Asin(ωx+φ)的形式,变形时利用诱导公式和二倍角公式逆用.
解答:解:(Ⅰ)∵f(x)=sin(π-ωx)cosωx+cos2ωx,
∴f(x)=sinωxcosωx+
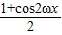
=
 sin2ωx+
sin2ωx+ cos2ωx+
cos2ωx+
=
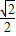 sin(2ωx+
sin(2ωx+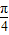 )+
)+
由于ω>0,依题意得
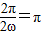 ,
,所以ω=1;
(Ⅱ)由(Ⅰ)知f(x)=
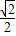 sin(2x+
sin(2x+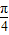 )+
)+ ,
,∴g(x)=f(2x)=
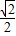 sin(4x+
sin(4x+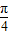 )+
)+
∵0≤x≤
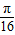 时,
时,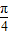 ≤4x+
≤4x+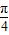 ≤
≤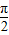 ,
,∴
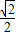 ≤sin(4x+
≤sin(4x+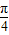 )≤1,
)≤1,∴1≤g(x)≤
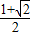 ,
,g(x)在此区间内的最小值为1.
点评:利用同角三角函数间的关系式可以化简三角函数式(1)化简的标准:第一,尽量使函数种类最少,次数最低,而且尽量化成积的形式;第二,能求出值的要求出值;第三,根号内的三角函数式尽量开出.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
