Question

设x、y满足约束条件分别求下列各式的最大值、最小值.(x、y均为整数)

(1)z=6x+10y;

(2)z=2x-y;

(3)z=2x-y.

Answer 1

解:(1)先作出可行域,如下图中△ABC表示的区域,且求得A(5,2)、B(1,1)、C(1,).

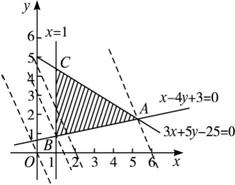
    作出直线l₀:6x+10y=0,再将直线l₀平移,当l₀的平行线l₁过B点时,可使z=6x+10y达到最小值,当l₀的平行线l₂过A点时,可使z=6x+10y达到最大值.

∴z_min=6×1+10×1=16;z_max=6×5+10×2=50.

(2)同上,作出直线l₀:2x-y=0,再将直线l₀平移,当l₀的平行线l₁过C点时,可使z=2x-y达到最小值,当l₀的平行线l₂过A点时,可使z=2x-y达到最大值.

∴z_max=8,z_min=-.

(3)同时,作出直线l₀:2x-y=0,再将直线l₀平移,当l₀的平行线l₂过A点时,可使z=2x-y达到最大值,z_max=8.当l₀的平行线l₁过C点时,可使z=2x-y达到最小值,但由于不是整数,而最优解(x,y)中,x、y必须都是整数,所以可行域内的点C(1,)不是最优解.当l₀的平行线经过可行域内的整点(1,4)时,可使z=2x-y达到最小值.

∴z_min=-2.