题目内容
已知i是虚数单位，z1=2+2i，z2=1-3i，那么复数z=
在复平面内对应的点位于（ ）
| ||
| z2 |
分析：先根据复数的基本运算对已知式子z进行化简，然后根据z=a+bi对应的点（a，b）所在的象限位置即可判断
解答：解：∵z1=2+2i，z2=1-3i，
∴z=
=
=
=
=
=-
+
i
∴在复平面内对应的点位于第二象限
故选B
∴z=
| ||
| z2 |
| (2+2i)2 |
| 1-3i |
| 8i |
| 1-3i |
| 8i(1+3i) |
| (1-3i)(1+3i) |
| -24+8i |
| 10 |
=-
| 12 |
| 5 |
| 4 |
| 5 |
∴在复平面内对应的点位于第二象限
故选B
点评：本题主要考查了复数的代数形式的乘除运算及复数与复平面的点的一一对应关系的应用，属于基础试题
练习册系列答案
相关题目
已知i是虚数单位，z=1-i，则
+z2对应的点所在的象限是（ ）
| 2 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
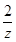＋z2对应的点所在的象限是