题目内容
关于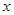
的一元二次不等式
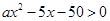的解集为
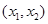，且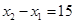
，则a=( )
A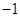． ; | B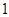． ; | C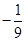． ; | D． ; |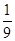
C
解析试题分析：因为关于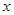的一元二次不等式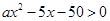的解集为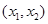，所以可知
<0.并且
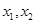是方程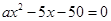
的两个根.由韦达定理可得
. 
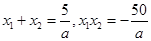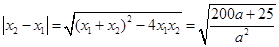=15.所以
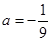或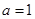
（舍去）.所以选C.
考点：1.二次不等式的解法.2.韦达定理.3.二次方程的解法.
练习册系列答案
相关题目
不等式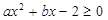
的解集为
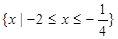，则实数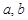
的值为（ ）
A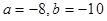． | B． |
C． | D． |
已知一元二次不等式
的解集为
,则
的解集为 （ ）
A． | B． |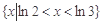
C． | D． |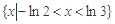
已知不等式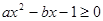
的解集是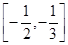
，则不等式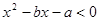
的解集是( )
A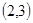． | B． |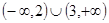
C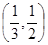． | D． |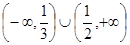
若不等式
对于一切非零实数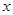
均成立，则实数
的取值范围是（ ）
A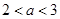． | B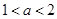． | C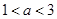． | D． |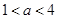
有甲、乙两个粮食经销商每次在同一粮食生产地以相同的价格购进粮食，他们共购进粮食两次，各次的粮食价格不同，甲每次购粮10000千克，乙每次购粮食10000元，在两次统计中，购粮的平均价格较低的是（ ）
| A．甲 | B．乙 | C．一样低 | D．不确定 |
不等式log2
≥1的解集为( )
| A．(－∞，－1] | B．[－1，＋∞) |
| C．[－1,0) | D．(－∞，－1]∪(0，＋∞) |
不等式2x2-x-1>0的解集是( )
A．（- ,1） |
| B．(1,+∞) |
| C．(-∞,1)∪(2,+∞) |
| D．（-∞,-）∪(1,+∞) |
设函数f(x)＝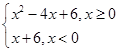
则不等式f(x)>f(1)的解集是( )．
| A．(－3,1)∪(3，＋∞) | B．(－3,1)∪(2，＋∞) |
| C．(－1,1)∪(3，＋∞) | D．(－∞，－3)∪(1,3) |