题目内容
【题目】在△ABC中，(1)已知a＝
，b＝
，B＝45°，求A、C、c；
(2)已知sin A∶sin B∶sin C＝(
＋1)∶(
－1)∶
，求最大角．
【答案】（1）A＝60°，C＝75°，c＝
，或A＝120°，C＝15°，c＝
. （2） 
【解析】试题分析：（1）由正弦定理求解即可，注意三角形解的个数的讨论；（2）由条件可判断C最大，设出三边，根据余弦定理求解。
试题解析：
(1)由正弦定理及已知条件有
＝
，
得sin A＝
，
∵a>b，
∴A>B＝45°，
∴A＝60°或120°.
①当A＝60°时，C＝180°－45°－60°＝75°，
∴c＝
＝
＝
，
②当A＝120°时，C＝180°－45°－120°＝15°，
∴c＝＝
＝
.
综上，A＝60°，C＝75°，c＝，或A＝120°，C＝15°，c＝.
(2)根据正弦定理可知a∶b∶c＝sin A∶sin B∶sin C＝(
＋1)∶(－1)∶
，
设
，
由余弦定理的推理得
，
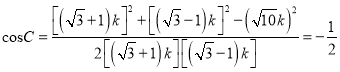又
，
∴
∴最大角为C且
．
练习册系列答案
阅读快车系列答案
相关题目
