题目内容
如图,向量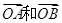 被矩阵M对应的变换
被矩阵M对应的变换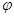 作用后分别变成
作用后分别变成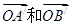 ,
,
(1)求矩阵M;(2)求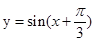 在
在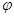 作用后的函数解析式.
作用后的函数解析式.
(1) ;(2)
;(2)
解析试题分析:(1)由矩阵与变换的知识可知:标变换公式 对应的矩阵为:
对应的矩阵为: ,即由矩阵
,即由矩阵 可将点(x,y)变换为点
可将点(x,y)变换为点 :满足
:满足 ;从而应用待定系数法,设出所要求的矩阵,再由已知条件代入即可列出方程组,解此方程组就可求出其对应的矩阵;(2)在函数
;从而应用待定系数法,设出所要求的矩阵,再由已知条件代入即可列出方程组,解此方程组就可求出其对应的矩阵;(2)在函数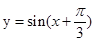 的图象上任取一点
的图象上任取一点 ,被
,被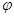 作用后的点为
作用后的点为 ,则有
,则有
 ,然后将x,y用含
,然后将x,y用含 的式子表示出来,由于点
的式子表示出来,由于点 在函数
在函数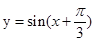 的图象上,将上式代入即得
的图象上,将上式代入即得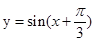 在
在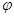 作用后的函数解析式.
作用后的函数解析式.
试题解析:(1)待定系数设M= ,由已知
,由已知 ,则有:
,则有:
 且
且
 即:
即: ,解得
,解得 ,从而有
,从而有 , 3分
, 3分
(2)在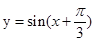 的图象上任取一点
的图象上任取一点 ,被
,被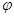 作用后的点为
作用后的点为 ,则
,则 ,代入
,代入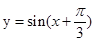 后得:
后得: 7分
7分
考点:1.矩阵的特征值;2.图象变换.

练习册系列答案
相关题目

 ,该方程组的解为
,该方程组的解为 ,则mn的值等于
,则mn的值等于  ,矩阵运算
,矩阵运算 都成立,则
都成立,则 .
.
 在矩阵C对应的变换作用下的曲线方程.
在矩阵C对应的变换作用下的曲线方程. ,若点P(1,1)在矩阵A对应的变换作用下得到点P′(0,-8).
,若点P(1,1)在矩阵A对应的变换作用下得到点P′(0,-8). ,若矩阵M的逆矩阵M-1=
,若矩阵M的逆矩阵M-1= ,求a、b的值.
,求a、b的值.
 =
= M
M 成立的矩阵M.
成立的矩阵M.