题目内容
设数列{an}满足a1=1,a2=2,对任意的n∈N*,an+2是an+1与an的等差中项.
(1)设bn=an+1-an,证明数列{bn}是等比数列,并求出其通项公式;
(2)写出数列{an}的通项公式(不要求计算过程),令 ,求数列{cn}的前n项和Sn.
,求数列{cn}的前n项和Sn.
解:(1)∵an+2是an+1与an的等差中项.
∴2an+2=an+1+an,
∵bn=an+1-an,∴bn+1=an+2-an+1= (an+1+an)-an+1=-
(an+1+an)-an+1=- bn,
bn,
∵a1=1,a2=2,
∴b1=a2-a1=1
∴数列{bn}是以1为首项,- 为公比的等比数列,通项公式为bn=
为公比的等比数列,通项公式为bn= ;
;
(2)由(1)知,an+1-an=
∴an=a1+(a2-a1)+…+(an-an-1)=1+1+…+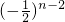 =
=
∴ =
=
∴Sn= +
+ +…+
+…+ ①
①
∴ Sn=
Sn= +
+ +…+
+…+ ②
②
①-②可得 Sn=1+
Sn=1+ +
+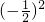 +…+
+…+ -
- =
=
∴数列{cn}的前n项和Sn= .
.
分析:(1)根据an+2是an+1与an的等差中项,可得2an+2=an+1+an,由bn=an+1-an,可得bn+1=an+2-an+1=- bn,从而可得数列{bn}是以1为首项,-
bn,从而可得数列{bn}是以1为首项,- 为公比的等比数列,可求通项公式;
为公比的等比数列,可求通项公式;
(2)利用累加法可得数列{an}的通项公式,进而可得 =
= ,利用错位相减法可求数列{cn}的前n项和.
,利用错位相减法可求数列{cn}的前n项和.
点评:本题考查数列递推式,考查等比数列的证明与通项,考查错位相减法求数列的和,属于中档题.
∴2an+2=an+1+an,
∵bn=an+1-an,∴bn+1=an+2-an+1=
 (an+1+an)-an+1=-
(an+1+an)-an+1=- bn,
bn,∵a1=1,a2=2,
∴b1=a2-a1=1
∴数列{bn}是以1为首项,-
 为公比的等比数列,通项公式为bn=
为公比的等比数列,通项公式为bn= ;
;(2)由(1)知,an+1-an=

∴an=a1+(a2-a1)+…+(an-an-1)=1+1+…+
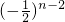 =
=
∴
 =
=
∴Sn=
 +
+ +…+
+…+ ①
①∴
 Sn=
Sn= +
+ +…+
+…+ ②
②①-②可得
 Sn=1+
Sn=1+ +
+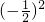 +…+
+…+ -
- =
=
∴数列{cn}的前n项和Sn=
 .
.分析:(1)根据an+2是an+1与an的等差中项,可得2an+2=an+1+an,由bn=an+1-an,可得bn+1=an+2-an+1=-
 bn,从而可得数列{bn}是以1为首项,-
bn,从而可得数列{bn}是以1为首项,- 为公比的等比数列,可求通项公式;
为公比的等比数列,可求通项公式;(2)利用累加法可得数列{an}的通项公式,进而可得
 =
= ,利用错位相减法可求数列{cn}的前n项和.
,利用错位相减法可求数列{cn}的前n项和.点评:本题考查数列递推式,考查等比数列的证明与通项,考查错位相减法求数列的和,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
设数列{an}满足a1=1,a2+a4=6,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
,则数列{cn}的前n项和Sn为( )
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|