题目内容
15.已知向量$\vec a$与向量$\vec b$夹角为$\frac{π}{6}$,且$|\vec a|=\sqrt{3}$,$\vec a⊥(\vec a-2\vec b)$,则$|\vec b|$=( )| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 1 | D. | 2 |
分析 $\vec a⊥(\vec a-2\vec b)$,可得$\overrightarrow{a}•(\overrightarrow{a}-2\overrightarrow{b})$=${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}$=0,代入解出即可.
解答 解:∵$\vec a⊥(\vec a-2\vec b)$,
∴$\overrightarrow{a}•(\overrightarrow{a}-2\overrightarrow{b})$=${\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}$=3-2$\sqrt{3}$$|\overrightarrow{b}|$×$cos\frac{π}{6}$=0,
解得$|\vec b|$=1.
故选:C.
点评 本题查克拉向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知A(1,2),B(-1,0),C(3,a)三点在同一条直线上,则a的值为( )
| A. | -2 | B. | 4 | C. | -4 | D. | 2 |
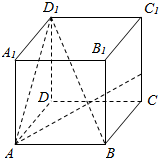 在棱长为4的正方体ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP.
在棱长为4的正方体ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP.