题目内容
已知Rt△ABC的直角顶点C在平面α内，斜边AB∥α，AB=2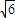
，AC、BC分别和平面α成45°和30°角，则AB到平面α的距离为
【答案】分析：分别过A、B向平面α引垂线AA′、BB′，垂足分别为A′、B′．设AA′=BB′=x，则在直角三角形ABC中分别表示出AC和BC，进而利用勾股定理求得x．
解答：
解：分别过A、B向平面α引垂线AA′、BB′，垂足分别为A′、B′．
设AA′=BB′=x，
则AC2=（
）2=2x2，
BC2=（
）2=4x2．
又AC2+BC2=AB2，
∴6x2=（2
）2，x=2．
故答案为2
点评：本题主要考查了点到面的距离计算．属基础题．
解答：
解：分别过A、B向平面α引垂线AA′、BB′，垂足分别为A′、B′．设AA′=BB′=x，
则AC2=（
）2=2x2，BC2=（
）2=4x2．又AC2+BC2=AB2，
∴6x2=（2
）2，x=2．故答案为2
点评：本题主要考查了点到面的距离计算．属基础题．
练习册系列答案
相关题目
