题目内容

已知函数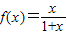．设数列{an}满足a1=1，an+1=f（an）（n∈N+）．
（1）求数列{an}的通项公式；
（2）已知数列{bn}满足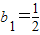，，求证：对一切正整数n≥1都有＜2．
【答案】分析：（1）由，an+1=f（an）（n∈N+）知：，由此能求出．
（2）由bn+1=（1+bn）2•，知bn+1=bn（bn+1），故=，由此利用裂项求法能够证明对一切正整数n≥1都有＜2．
解答：（1）解：∵，an+1=f（an）（n∈N+），
∴，…1分
=，…..3分
=1，…5分
∴{}是以为首项，1为公差的等差数列，
即，
∴．…6分
（2）证明：由已知得bn+1=（1+bn）2•，
∴bn+1=bn（bn+1），显然bn∈（0，+∞），…7分
∴=====，…9分
∴
=（）+（）+…+（）
=
=2-＜2．…11分
所以，对一切正整数n≥1都有＜2．…12分
点评：本题考查数列的通项公式的求法和不等式的证明，解题时要认真审题，仔细解答，注意裂项求和法的合理运用．
练习册系列答案
相关题目
已知函数f（x）=ax+b，当x∈[a1，b1]时值域为[a2，b2]，当x∈[a2，b2]时值域为[a3，b3]，当x∈[an-1，bn-1]时值域为[an，bn]…其中a、b为常数，a1=0，b1=1
（1）若a=1，b=2，求数列{an}和{bn}的通项公式．
（2）若a＞0，a≠1，要使数列{bn}是公比不为1的等比数列，求b的值．
（3）若a＞0，设数列{an}和{bn}的前n项和分别为Sn和Tn，求Tn-Sn的值．
已知函数f(x)=
x+1-aa-x
，a∈R．利用函数y=f（x）构造一个数列{xn}，方法如下：对于定义域中给定的x1，令x2=f（x1），x3=f（x2），…，xn=f（xn-1）（n∈N*），…如果取定义域中任一值作为x1，都可以用上述方法构造出一个无穷数列{xn}．
（1）求实数a的值；
（2）若x1=1，求（x1+1）（x2+1）…（xn+1）的值；
（3）设Tn=（x1+1）（x2+1）…（xn+1）（n∈N*），试问：是否存在n使得Tn+Tn+1+…+Tn+2006=2006成立，若存在，试确定n及相应的x1的值；若不存在，请说明理由？
（2009•嘉定区一模）（理）已知函数f(x)=log2
2
x
1-x
，P1（x1，y1）、P2（x2，y2）是f（x）图象上两点．
（1）若x1+x2=1，求证：y1+y2为定值；
（2）设Tn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)，其中n∈N*且n≥2，求Tn关于n的解析式；
（3）对（2）中的Tn，设数列{an}满足a1=2，当n≥2时，an=4Tn+2，问是否存在角a，使不等式(1-
1
a1
)(1-
1
a2
)…(1-
1
an
)＜
sinα
2n+1
对一切n∈N*都成立？若存在，求出角α的取值范围；若不存在，请说明理由．

已知函数f(x)＝(a，b为常数，a≠0)，满足f(2)＝1，且f(x)＝x有两个相同的根．

(1)求f(x)的表达式；

(2)设数列{xn}满足xn+1＝f(xn)，且x1＞0，证明数列{}是等差数列．

已知函数．

(Ⅰ)设{an}是正数组成的数列，前n项和为Sn，其中a1＝3．若点(n∈N*)在函数y＝的图象上，求证：点(n，Sn)也在y＝的图象上；

(Ⅱ)求函数f(x)在区间(a－1，a)内的极值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网