Question

如图所示，△VAD是等边三角形，ABCD是矩形，，平面VAD⊥平面ABCD，F为AB中点。

（1）求VC与平面ABCD所成角的大小；

（2）当V到平面ABCD的距离为3时，求B到平面VFC的距离。

Answer 1

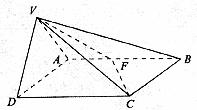
解：解法一：（1）取AD中点E，连接VE、EC，

    ∵△VAD为等边三角形，∴ VE⊥AD，

又平面VAD⊥平面ABCD，∴ VE⊥平面ABCD。

∴∠VCE为直线VC与平面ABCD所成的角。

，

∴，∴。

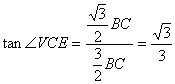即直线VC与平面ABCD所成的角为。

（2）∵，∴，

∴

的面积，

，

，

，

∴，

，

即B到平面VFC的距离为。

解法二：取AD中点E，连接VE，EC，取BC中点G，连接EG，设BC＝a，则。

以E为原点，为轴，为轴，为轴建立空间直角坐标系．得：

则，，

设面VFC的一个法向量

∴

∴，

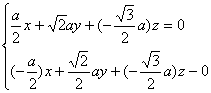
B到平面VFC的距离为：。