题目内容
(本题满分16分)
已知等差数列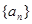 的前
的前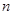 项和为
项和为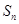 ,且
,且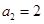 ,
,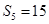 ,数列
,数列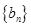 满足:
满足:
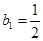 ,
,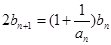 ,
,
(1)求数列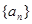 、
、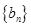 的通项公式;
的通项公式;
(2)设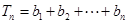 ,
,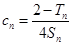 ,证明:
,证明:
已知等差数列
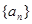 的前
的前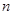 项和为
项和为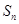 ,且
,且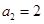 ,
,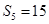 ,数列
,数列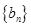 满足:
满足: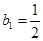 ,
,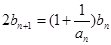 ,
,(1)求数列
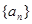 、
、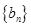 的通项公式;
的通项公式;(2)设
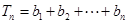 ,
,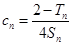 ,证明:
,证明:
(1) ,
, (2)根据错位相减法来进行求和,得到
(2)根据错位相减法来进行求和,得到 ,然后借助于
,然后借助于 来证明。
来证明。
 ,
, (2)根据错位相减法来进行求和,得到
(2)根据错位相减法来进行求和,得到 ,然后借助于
,然后借助于 来证明。
来证明。试题分析:解:(1)由题意得
 ,解得
,解得 ∴
∴ …………………3分
…………………3分由
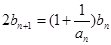 ,得
,得 ,
, ∴数列
 是等比数列,其中首项
是等比数列,其中首项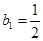 ,公比
,公比 ,
, ∴
 . ……………………6分
. ……………………6分注:也可以累乘处理
(2)
 ①,
①, ②
②∴②-①得:

∴
 ………………9分
………………9分∴

∴
 ……………………16分
……………………16分点评:该试题涉及了数列的通项公式和数列求和的运用。解决的关键是熟练的运用等差数列和等比数列的通项公式来求解通项公式,同时能根据错位相减法求和,属于中档题。

练习册系列答案
相关题目
 的前
的前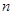 项和为
项和为 ,满足
,满足 .
. 为等比数列;
为等比数列; 满足
满足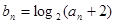 ,
, 为数列
为数列 的前
的前 .
.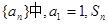 是数列
是数列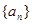 的前n项和,对任意
的前n项和,对任意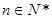 ,有2Sn=2
,有2Sn=2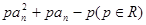 .
.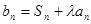 ,(
,(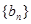 从第二项起每一项都比它的前一项大,求
从第二项起每一项都比它的前一项大,求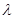 的取值范围.
的取值范围.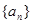 的前
的前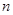 项和为
项和为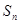 ,且
,且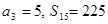 .
.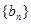 满足:
满足: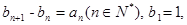 求数列
求数列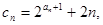 求数列
求数列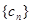 的前
的前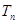 .
.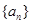 是递增的等差数列,
是递增的等差数列,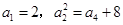 .
.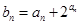 ,求数列
,求数列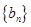 的前
的前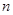 项和
项和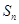 .
.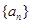 共有
共有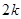 项(整数
项(整数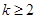 ),首项
),首项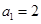 ,设该数列的前
,设该数列的前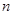 项和为
项和为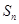 ,且
,且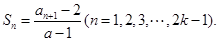 其中常数
其中常数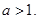 ⑴求
⑴求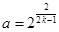 ,数列
,数列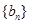 满足
满足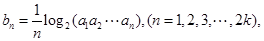
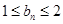 ;
;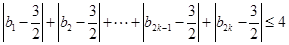 ,求
,求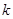 的最大值.
的最大值.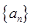 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数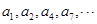 构成等差数列
构成等差数列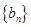 ,
,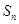 是
是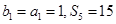
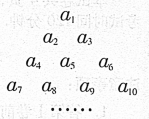
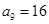 ,求
,求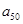 的值;
的值;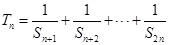 ,求
,求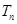 .
.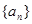 的前n项和为
的前n项和为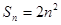
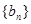 为等比数列,且
为等比数列,且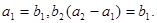
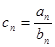 ,求数列
,求数列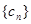 的前n项和
的前n项和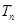 。
。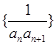 的前100项和为( )
的前100项和为( )


