题目内容
 如图,有一圆盘,其中阴影部分的圆心角为45°,向圆盘内投镖,如果某人每次都投入圆盘内,那么他投中阴影部分的概率为
如图,有一圆盘,其中阴影部分的圆心角为45°,向圆盘内投镖,如果某人每次都投入圆盘内,那么他投中阴影部分的概率为
- A.

- B.

- C.

- D.

A
分析:要计算投中阴影部分的概率,根据每次都投镖都能投入圆盘内,圆盘对应的圆心角的度数为360°,阴影部分的圆心角为45°,代入几何概型概率公式,即可得到答案.
解答:圆盘对应的圆心角的度数为360°,
阴影部分的圆心角为45°
故投中阴影部分的概率P=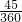 =
= .
.
故选A
点评:本题考查的知识点是几何概型,找出基本事件对应的几何量是圆心角为360°的角度,满足条件的几何量是圆心角为45°的角度,是解答本题的关键,本题也可利用面积计算,即基本事件总数对应圆面积,满足条件的基本事件对应几何量为扇形面积.
分析:要计算投中阴影部分的概率,根据每次都投镖都能投入圆盘内,圆盘对应的圆心角的度数为360°,阴影部分的圆心角为45°,代入几何概型概率公式,即可得到答案.
解答:圆盘对应的圆心角的度数为360°,
阴影部分的圆心角为45°
故投中阴影部分的概率P=
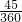 =
= .
.故选A
点评:本题考查的知识点是几何概型,找出基本事件对应的几何量是圆心角为360°的角度,满足条件的几何量是圆心角为45°的角度,是解答本题的关键,本题也可利用面积计算,即基本事件总数对应圆面积,满足条件的基本事件对应几何量为扇形面积.

练习册系列答案
相关题目
 如图,有一圆盘,其中阴影部分的圆心角为45°,向圆盘内投镖,如果某人每次都投入圆盘内,那么他投中阴影部分的概率为( )
如图,有一圆盘,其中阴影部分的圆心角为45°,向圆盘内投镖,如果某人每次都投入圆盘内,那么他投中阴影部分的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,有一圆盘,其中的阴影部分圆心角为45°,若向圆内投镖,则投中阴影部分的概率为
如图,有一圆盘,其中的阴影部分圆心角为45°,若向圆内投镖,则投中阴影部分的概率为









