题目内容
(本小题满分12分)
如图,台风中心从A地以每小时20千米的速度向东北方向(北偏东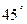 )移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
)移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
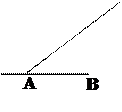
(1) 求台风移动路径所在的直线方程;
(2)求城市B处于危险区域的时间是多少小时?
如图,台风中心从A地以每小时20千米的速度向东北方向(北偏东
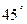 )移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题:
)移动,离台风中心不超过300千米的地区为危险区域.城市B在A地的正东400千米处.请建立恰当的平面直角坐标系,解决以下问题: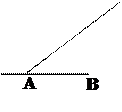
(1) 求台风移动路径所在的直线方程;
(2)求城市B处于危险区域的时间是多少小时?
.解:
法一、
(1)以B为原点,正东方向为 轴建立如图所示的直角坐标系,
轴建立如图所示的直角坐标系,
则台风中心A的坐标是(-400,0 ),台风移动路径所在的直线方程为
),台风移动路径所在的直线方程为
(2)以B为圆心,300千米为半径作圆,和直线 相交于
相交于 、
、 两点.可以认为,台风中心移到
两点.可以认为,台风中心移到 时,城市B开始受台风影响(危险区),直到
时,城市B开始受台风影响(危险区),直到 时,解除影响.
时,解除影响.
因为点B到直线 的距离
的距离 ,
,
所以 ,
,
而 (小时).所以B城市处于危险区内的时间是10小时.
(小时).所以B城市处于危险区内的时间是10小时.
法二、以A为原点,正东方向为 轴建立直角坐标系,
轴建立直角坐标系,
则台风移动路径所在的直线方程为 ,以B为圆心,300千米为半径作圆,
,以B为圆心,300千米为半径作圆,
则圆方程为 ,以下思路类似法一.
,以下思路类似法一.
法一、
(1)以B为原点,正东方向为
 轴建立如图所示的直角坐标系,
轴建立如图所示的直角坐标系,则台风中心A的坐标是(-400,0
 ),台风移动路径所在的直线方程为
),台风移动路径所在的直线方程为
(2)以B为圆心,300千米为半径作圆,和直线
 相交于
相交于 、
、 两点.可以认为,台风中心移到
两点.可以认为,台风中心移到 时,城市B开始受台风影响(危险区),直到
时,城市B开始受台风影响(危险区),直到 时,解除影响.
时,解除影响.因为点B到直线
 的距离
的距离 ,
,所以
 ,
, 而
 (小时).所以B城市处于危险区内的时间是10小时.
(小时).所以B城市处于危险区内的时间是10小时. 法二、以A为原点,正东方向为
 轴建立直角坐标系,
轴建立直角坐标系,则台风移动路径所在的直线方程为
 ,以B为圆心,300千米为半径作圆,
,以B为圆心,300千米为半径作圆,则圆方程为
 ,以下思路类似法一.
,以下思路类似法一.略

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 ABC中角A,B,C的对边分别为a,b,c,且满足(2a-c)cosB=bcosC
ABC中角A,B,C的对边分别为a,b,c,且满足(2a-c)cosB=bcosC n>1恒成立,求k的取值范围.
n>1恒成立,求k的取值范围.
 是( )
是( ) 中,
中,
 ( )
( )



 B=120°,则△ABC的面积为( )
B=120°,则△ABC的面积为( )
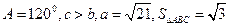 ,求
,求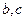 .
. 中,a=2
中,a=2 b="6 " B=60
b="6 " B=60 则 C等于 ( )
则 C等于 ( )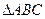 中,角
中,角 所对的边分别是
所对的边分别是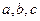 ,若
,若
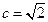 ,求
,求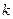 的值.
的值.