题目内容
6.设α,β,γ是三个互不重合的平面,m,n是两条不重合的直线,下列命题中正确的是( )| A. | 若α⊥β,β⊥γ,则α⊥γ | B. | 若m∥α,n∥β,α⊥β,则m⊥n | ||
| C. | 若α⊥β,m?β,m⊥α,则m∥β | D. | 若α∥β,m∥α,则m∥β |
分析 根据空间直线,平面直线平行或垂直的判定定理和性质定理进行判断即可.
解答 解:A.同时垂直于一个平面的两个平面不一定垂直,可能平行也可能相交,故A错误,
B.若m∥α,n∥β,α⊥β,则m,n关系不确定,故B错误,
C.若α⊥β,m?β,m⊥α,则m∥β,成立,
D.若α∥β,m∥α,则m∥β或m?β,故D错误,
故选:C
点评 本题主要考查空间直线和平面直线平行或垂直的判断,利用相应的判定定理和性质定理是解决本题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
9.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则点C到平面BC1D的距离等于( )
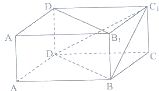

| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{9}$ |
10.函数f(x)=x2-1,则f(1)=( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
11.已知焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{9}$=1的离心率是e=$\frac{1}{2}$,则a的值为( )
| A. | 3$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 12 |