题目内容
如图所示,n台机器人M1,M2,……,Mn位于一条直线上,检测台M在线段M1 Mn上,n台机器人需把各自生产的零件送交M处进行检测,送检程序设定:当Mi把零件送达M处时,Mi+1即刻自动出发送检(i=1,2,……,n-1)已知Mi的送检速度为V(V>0), 且 记
记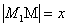 ,n台机器人送检时间总和为f(x).
,n台机器人送检时间总和为f(x).
 |
(1)求f(x)的表达式;
(2)当n=3时,求x的值使得f(x)取得最小值;
(3)求f(x)取得最小值时, x的取值范围。
(1)以M1为坐标原点,M1,M2…,Mn所在直线为x轴建立数轴Mi的坐标为i-1,M的坐标为x。
f(x)= 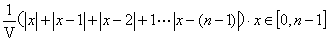 …3分
…3分
(2)n=3时,V f(x)=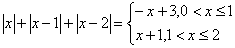
 f(x)在x=1处取得最小值
f(x)在x=1处取得最小值
(3)当i≤x≤i+1,(0≤i<n-2, i∈Ζ)时。
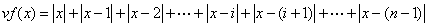
=x+(x-1)+…+(x-i)-(x-(i+1))+…+(x-(n-1))
=[( i+1)x-(1+2+…+ i)]-[n-( i+1)·x-( i+1+ i+2+…+(n-1) ]
=-[n-2 (i+1) ]·x-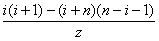
当0≤i<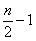 时,f(x)单调递减:当
时,f(x)单调递减:当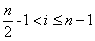 时,f(x)单调递增
时,f(x)单调递增
当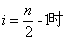 , f(x)为常函数,又f(x)图象是一条连续不断的图象,所以①n为偶数时,f(x)在(0,
, f(x)为常函数,又f(x)图象是一条连续不断的图象,所以①n为偶数时,f(x)在(0,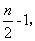 )内单调递减,在(
)内单调递减,在(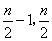 )为常函数,在(
)为常函数,在(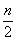 ,n-1)单调递增,所以当x∈[
,n-1)单调递增,所以当x∈[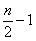 ,
,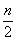 ]时f(x)取得最小值。
]时f(x)取得最小值。
②n为奇数时,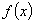 在
在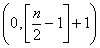 内单调递减,(
内单调递减,(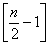 表示
表示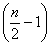 的整数部分),在
的整数部分),在 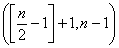 内单调递增,所以当
内单调递增,所以当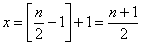 时
时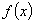 取得最小值 (13分)
取得最小值 (13分)

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 中,两直角边分别为
中,两直角边分别为 设
设 为斜边上的高,则
为斜边上的高,则 ;由此类比三棱锥
;由此类比三棱锥 中的三条侧棱
中的三条侧棱 两两垂直,且长度分别为
两两垂直,且长度分别为 ,设棱锥底面
,设棱锥底面 上的高为
上的高为 (
( 为参数)与曲线
为参数)与曲线  (
( 为参数)的交点个数
为参数)的交点个数 ,若
,若 为实数,
为实数, ∥
∥ ,则
,则 B、
B、 C、1 D、2
C、1 D、2 ∈N*,定义
∈N*,定义 ,其中K是满足
,其中K是满足 的最大整数,[x]表示不超过x的最大整数,如
的最大整数,[x]表示不超过x的最大整数,如 ,则
,则 。
。 的最大整数m为 。
的最大整数m为 。 ,若
,若 ,则a=
,则a= B、
B、 C、1 D、2
C、1 D、2 。
。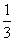 x3-x2+ax-5在区间[-1,2]上不单调,则实数a的取值范围是______.
x3-x2+ax-5在区间[-1,2]上不单调,则实数a的取值范围是______.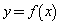 是奇函数,当
是奇函数,当 时,
时,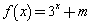 ,若
,若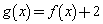 ,则
,则