题目内容
下列命题:①若f(x)是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,θ∈(![]() ,
,![]() ),则f(sinθ)>f(cosθ);
),则f(sinθ)>f(cosθ);
②若锐角α、β满足cosα>sinβ,则α+β<![]() ;
;
③若f(x)=2cos2![]() -1,则f(x+π)=f(x)对x∈R恒成立;
-1,则f(x+π)=f(x)对x∈R恒成立;
④要得到函数y=sin(![]() )的图象,只需将y=sin
)的图象,只需将y=sin![]() 的图象向右平移
的图象向右平移![]() 个单位.
个单位.
其中真命题的个数为
A.1 B.2 C.3 D.4
A 对于①:由题意知,f(x)在[0,1]上是减函数,又θ∈(![]() ,
,![]() ),∴sinθ>cosθ.
),∴sinθ>cosθ.
∴f(sinθ)<f(cosθ).故①错误;
对于②:锐角α、β满足cosα>sinβ,即sin(![]() -α)>sinβ.
-α)>sinβ.
又0<![]() -α<
-α<![]() ,0<β<
,0<β<![]() ,且y=sinx在(0,
,且y=sinx在(0,![]() )上单调递增,
)上单调递增,
∴![]() -α>β,即α+β<
-α>β,即α+β<![]() .故②正确.
.故②正确.
对于③:f(x)=2cos2![]() -1=cosx,f(x)的最小正周期T=2π,显然f(x+π)=f(x)不恒成立.故③错误.
-1=cosx,f(x)的最小正周期T=2π,显然f(x+π)=f(x)不恒成立.故③错误.
对于④:将y=sin![]() 的图象向右平移
的图象向右平移![]() 个单位,得y=sin
个单位,得y=sin![]() (x
(x![]() )=sin(
)=sin(![]() x
x![]() ),而不是y=sin(
),而不是y=sin(![]()
![]() ).故④错误.
).故④错误.
因此真命题的个数有1个.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
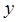 轴对称;
轴对称;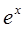 ,则
,则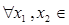
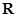 ,都有
,都有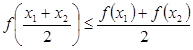 ;
;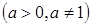 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,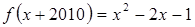 (x∈
(x∈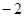 .
.