题目内容
【题目】已知平面向量 ![]() ,
, ![]() ,
, ![]() 满足|
满足| ![]() |=
|= ![]() ,|
,| ![]() |=1,
|=1, ![]()
![]() =﹣1,且
=﹣1,且 ![]() ﹣
﹣ ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为
的夹角为 ![]() ,则|
,则| ![]() |的最大值为( )
|的最大值为( )
A.![]()
B.2 ![]()
C.![]()
D.4
【答案】A
【解析】解:设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() . ∵平面向量
. ∵平面向量 ![]() ,
, ![]() ,
, ![]() 满足|
满足| ![]() |=
|= ![]() ,|
,| ![]() |=1,
|=1, ![]()
![]() =﹣1,
=﹣1,
∴cos< ![]() >=
>= ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
∴< ![]() >=
>= ![]() .
.
∵ ![]() ﹣
﹣ ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为
的夹角为 ![]() ,
,
∴点C在△OAB的外接圆的弦AB所对的优弧上,如图所示.
因此| ![]() |的最大值为△OAB的外接圆的直径.
|的最大值为△OAB的外接圆的直径.
∵| ![]() ﹣
﹣ ![]() |=
|= ![]() =
= ![]() =
= ![]() .
.
由正弦定理可得:△OAB的外接圆的直径2R= ![]() =
= ![]() =
= ![]() ,
,
则| ![]() |的最大值为
|的最大值为 ![]() .
.
故选:A.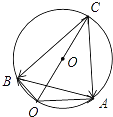

练习册系列答案
相关题目
