题目内容
已知点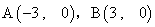 ,动点P 满足:|PA|=2|PB|.
,动点P 满足:|PA|=2|PB|.
(1)若点P的轨迹为曲线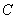 ,求此曲线的方程;
,求此曲线的方程;
(2)若点Q在直l1: x+y+3=0上,直线l2经过点Q且与曲线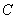 只有一个公共点M,求|QM|的最小值。
只有一个公共点M,求|QM|的最小值。
已知点 ,动点P 满足:|PA|=2|PB|.
,动点P 满足:|PA|=2|PB|.
(1) 若点P的轨迹为曲线C,求此曲线的方程;
(2) 若点Q在直l1: x+y+3=0上,直线l2经过点Q且与曲线C只有一个公共点M,求|QM|的最小值。
解:(1)设P点的坐标为(x,y), 由|PA|=2|PB|,得
 =2
=2
化简,得
即为所求。
曲线C是以点(5,0)为圆心,4为半径的圆。直线l2是圆的切线,连接CQ,则
|QM|= =
=
当CQ  l1 ,|CQ|取最小值,则|CQ|min=
l1 ,|CQ|取最小值,则|CQ|min=
此时|QM|的最小值为 = 4
= 4

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,BC=2,则C=___________.
,BC=2,则C=___________. 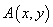 在圆
在圆 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间
上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间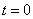 时,点
时,点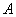 的坐标是
的坐标是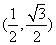 ,则当
,则当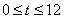 时,动点
时,动点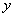 关于
关于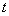 (单位:秒)的函数的单调递增区间是 ( )
(单位:秒)的函数的单调递增区间是 ( ) 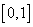 B.
B.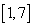 C.
C.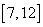 D.
D.
 +2
+2 +3上的点,且曲线C在点P处切线倾斜角的取值范围是
+3上的点,且曲线C在点P处切线倾斜角的取值范围是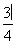 ,
, ),则点P横坐标的取值范围为
),则点P横坐标的取值范围为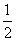 B.-
B.-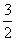 ,-1) C.0,1) D.
,-1) C.0,1) D. =2;
=2; 上任取一个实数
上任取一个实数 ,则事件“
,则事件“ ”发生的概率是
”发生的概率是 B.
B.  C.
C.  D.
D. 
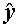 =0.85x-85.71,则下列结论中不正确的是( )
=0.85x-85.71,则下列结论中不正确的是( )