题目内容

已知a≠0，函数

（Ⅰ）求函数的单调递减区间；

解：（Ⅰ）由求导得，′…………………2分

①当＞0时，由′＜0，解得0＜＜

所以在（0，）上递减.…………………………………4分

②当＜0时，由′＜0，可得＜＜0

所以在（，0）上递减.……………………………………6分

综上，当a＞0时，f(x)单调递减区间为（0，）；

当a＜0时，f(x)单调递减区间为（，0）……………………………………………7分

（Ⅱ）设  ∈(0,］.

对F(x)求导，得F′………………………………8分

因为∈(0,],a＞0，所以F′＞0，………………………10分

F（x）在区间(0,]上为增函数，则……………………………11分

   依题意，只需＞0，即＞0，

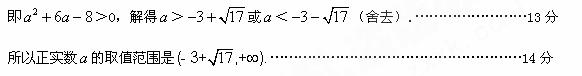
练习册系列答案
相关题目
已知a≥0，函数f（x）=（x2-2ax）ex．
（Ⅰ）当x为何值时，f（x）取得最小值？证明你的结论；
（Ⅱ）设f（x）在[-1，1]上是单调函数，求a的取值范围．
已知a≠0，函数f(x)=
1
3
a2x3-ax2+
2
3
，g（x）=-ax+1，x∈R．
（I）求函数f（x）的单调递减区间；
（Ⅱ）若在区间(0，
1
2
]上至少存在一个实数x0，使f（x0）＞g（x0）成立，试求正实数a的取值范围．
已知a≥0，函数f（x）=x2+ax．设x1∈(-∞，-
a
2
)，记曲线y=f（x）在点M（x1，f（x1））处的切线为l，l与x轴的交点是N（x2，0），O为坐标原点．
（Ⅰ）证明：x2=
x
2
1
2x1+a
；
（Ⅱ）若对于任意的x1∈(-∞，-
a
2
)，都有
OM
•
ON
＞
9a
16
成立，求a的取值范围．
已知a≥0，函数f（x）=（x2-2ax）ex．
（1）当a=0时讨论函数的单调性；
（2）当x取何值时，f（x）取最小值，证明你的结论．
已知a≥0，函数f(x)=a2+
2
cos(x-
π
4
)+
1
2
sin2x的最大值为
25
2
，则实数a的值是
12-2
2
12-2
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网