题目内容
设函数y=（x）是定义在R+上的减函数，并且满足f（xy）=f（x）+f（y），f（
）=1，
（1）求f（1）的值
（2）如果f（x）+f（
-x）≤2，求x的值．
| 1 |
| 3 |
（1）求f（1）的值
（2）如果f（x）+f（
| 2 |
| 3 |
令x=y=1则f（1x1）=f（1）+f（1），故f（1）=0
（2）由题意知x＞0，且
-x＞0，
而f（x）+f（
-x）=f[x（
-x）]≤f（
）+f（
）=f（
）
因为函数y=f（x）是定义在R+上的减函数，
故x（
-x）≥
，故x=
∈（0，
）．
∴x=
．
（2）由题意知x＞0，且
| 2 |
| 3 |
而f（x）+f（
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
因为函数y=f（x）是定义在R+上的减函数，
故x（
| 2 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 2 |
| 3 |
∴x=
| 1 |
| 3 |
练习册系列答案
相关题目
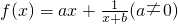的图象过点（0，-1）且与直线y=-1有且只有一个公共点；设点P（x0，y0）是函数y=f（x）图象上任意一点，过点P分别作直线y=x和直线x=1的垂线，垂足分别是M，N．
(a,b∈Z)，曲线y=f(x)在点（2，f(2)）处的切线方程为y=3。
(a,b∈Z)，曲线y=f(x)在点（2，f(2)）处的切线方程为y=3。