题目内容
【题目】已知函数f(x)=alnx+(x﹣c)|x﹣c|,a<0,c>0.
(1)当a=﹣ ![]() ,c=
,c= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)当c= ![]() +1时,若f(x)≥
+1时,若f(x)≥ ![]() 对x∈(c,+∞)恒成立,求实数a的取值范围;
对x∈(c,+∞)恒成立,求实数a的取值范围;
(3)设函数f(x)的图象在点P(x1 , f(x1))、Q(x2 , f(x2))两处的切线分别为l1、l2 . 若x1= ![]() ,x2=c,且l1⊥l2 , 求实数c的最小值.
,x2=c,且l1⊥l2 , 求实数c的最小值.
【答案】
(1)解:函数 ![]() ,求导得
,求导得 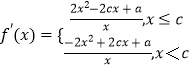
当 ![]() ,
, ![]() 时,
时, 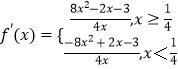 ,
,
若 ![]() ,则
,则 ![]() 恒成立,所以f(x)在
恒成立,所以f(x)在 ![]() 上单调减;
上单调减;
若 ![]() ,则
,则 ![]() ,令f′(x)=0,解得
,令f′(x)=0,解得 ![]() 或
或 ![]() (舍),
(舍),
当 ![]() 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在 ![]() 上单调减;
上单调减;
当 ![]() 时,f′(x)>0,f(x)在
时,f′(x)>0,f(x)在 ![]() 上单调增.
上单调增.
所以函数f(x)的单调减区间是 ![]() ,单调增区间是
,单调增区间是 ![]()
(2)解:当x>c, ![]() 时,
时, ![]() ,而
,而 ![]() ,所以
,所以
当c<x<1时,f′(x)<0,f(x)在(c,1)上单调减;
当x>1时,f′(x)>0,f(x)在(1,+∞)上单调增.
所以函数f(x)在(c,+∞)上的最小值为 ![]() ,
,
所以 ![]() 恒成立,解得a≤﹣1或a≥1,
恒成立,解得a≤﹣1或a≥1,
又由 ![]() ,得a>﹣2,所以实数a的取值范围是(﹣2,﹣1]
,得a>﹣2,所以实数a的取值范围是(﹣2,﹣1]
(3)解:由l1⊥l2知, ![]() ,而
,而 ![]() ,则
,则 ![]() ,
,
若 ![]() ,则
,则 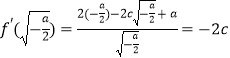 ,所以
,所以 ![]() ,
,
解得 ![]() ,不符合题意;
,不符合题意;
故 ![]() ,则
,则 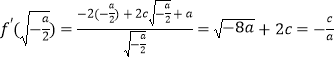 ,
,
整理得, ![]() ,由c>0得,
,由c>0得, ![]() ,
,
令 ![]() ,则
,则 ![]() ,t>2,所以
,t>2,所以 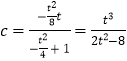 ,
,
设 ![]() ,则
,则 ![]() ,
,
当 ![]() 时,g′(t)<0,g(t)在
时,g′(t)<0,g(t)在 ![]() 上单调减;
上单调减;
当 ![]() 时,g′(t)>0,g(t)在
时,g′(t)>0,g(t)在 ![]() 上单调增.
上单调增.
所以,函数g(t)的最小值为 ![]() ,故实数c的最小值为
,故实数c的最小值为 ![]()
【解析】(1)求函数的导数,利用函数单调性和导数之间的关系,即可求f(x)的单调区间;(2)若f(x)≥ ![]() 对x∈(c,+∞)恒成立,则只需求出f(x)的最小值即可;(3)由l1⊥l2知,
对x∈(c,+∞)恒成立,则只需求出f(x)的最小值即可;(3)由l1⊥l2知, ![]() ,得到
,得到 ![]() ,分类讨论,再由导数与单调性的关系,即可得到实数c的最小值.
,分类讨论,再由导数与单调性的关系,即可得到实数c的最小值.
【考点精析】掌握利用导数研究函数的单调性和函数的极值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案