题目内容
过点(0,-4)与曲线y=x3+x-2相切的直线方程是分析:设出所求切线方程的切点坐标和斜率,把切点坐标代入曲线方程得到一个等式记作①,然后求出曲线方程的导函数,把设出的切点的横坐标代入导函数即可表示出切线的斜率,根据切点坐标和斜率写出切线的方程,把切点坐标代入又得到一个等式,记作②,联立①②即可求出切点的横坐标,进而得到切线的斜率,根据已知点的坐标和求出的斜率写出切线方程即可.
解答:解:设切点坐标为(x1,y1),过(0,-4)切线方程的斜率为k,
则y1=x13+x1-2①,
又因为y′=3x2+1,所以k=y′x=x1=3x12+1,
则过点(0,-4)与曲线y=x3+x-2相切的直线方程是:y=(3x12+1)x-4,
则y1=(3x12+1)x1-4②,
由①和②得:x13+x1-2=(3x12+1)x1-4,化简得:2x13=2,解得x1=1,
所以过点(0,-4)与曲线y=x3+x-2相切的直线方程是:y=4x-4.
故答案为:y=4x-4
则y1=x13+x1-2①,
又因为y′=3x2+1,所以k=y′x=x1=3x12+1,
则过点(0,-4)与曲线y=x3+x-2相切的直线方程是:y=(3x12+1)x-4,
则y1=(3x12+1)x1-4②,
由①和②得:x13+x1-2=(3x12+1)x1-4,化简得:2x13=2,解得x1=1,
所以过点(0,-4)与曲线y=x3+x-2相切的直线方程是:y=4x-4.
故答案为:y=4x-4
点评:此题考查学生会利用导数求曲线上过某点切线方程的斜率,会根据一点坐标和斜率写出直线的方程,是一道综合题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
.(本小题满分14分)
已知椭圆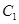 、抛物线
、抛物线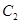 的焦点均在
的焦点均在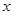 轴上,
轴上,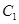 的中心和
的中心和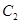 的顶点均为原点
的顶点均为原点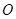 ,从每条曲
,从每条曲
线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(Ⅰ)求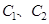 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线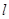 满足条件:①过
满足条件:①过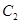 的焦点
的焦点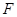 ;②与
;②与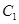 交不同两点
交不同两点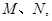 且满
且满
足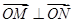 ?若存在,求出直线
?若存在,求出直线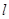 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
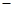 2
2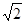
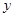
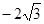
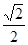
 +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).