题目内容
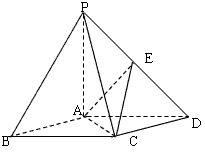
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=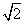 a,点E是PD的中点,
a,点E是PD的中点,
(Ⅰ)证明PA⊥平面ABCD,PB∥平面EAC;
(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的正切值。
|
(Ⅰ)证明:因为底面ABCD是菱形,∠ABC=60°, |
|
| (Ⅱ)解:作EG∥PA交AD于G, 由PA⊥平面ABCD,知EG⊥平面ABCD, 作GH⊥AC于H,连结EH, 则EH⊥AC,∠EHG即为二面角θ的平面角, 又E是PD的中点,从而G是AD的中点,  , ,所以  。 。 |
 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
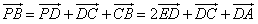
 ,
, 共面,
共面, 平面EAC,
平面EAC, 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.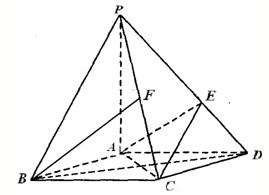 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2