题目内容
在△ABC中,a,b,c分别为角A,B,C的对边,设 f(x)=a2x2-(a2-b2)x-4c2.
(1)若 f(1)=0,且B-C=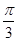 ,求角C;
,求角C;
(2)若 f(2)=0,求角C的取值范围.
【答案】
解:(1)由 f(1)=0,得a2-a2+b2-4c2=0,∴b=2c -----------2分
又由正弦定理,得b=2RsinB,c=2RsinC,
将其代入上式,得sinB=2sinC --------------------------4分
∵B-C=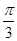 ∴B=
∴B=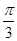 +C,将其代入上式,得sin(
+C,将其代入上式,得sin(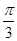 +C)=2sinC
+C)=2sinC
∴sin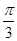 cosC+cos
cosC+cos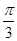 sinC=2sinC,
-----------------------------5分
sinC=2sinC,
-----------------------------5分
整理得,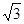 sinC=cosC
------------------------- --------6分
sinC=cosC
------------------------- --------6分
∴tanC=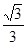
∵角C是三角形的内角,∴C=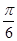 ---------------8分
---------------8分
(2)∵ f(2)=0,∴4a2-2a2+2b2-4c2=0,即a2+b2-2c2=0 ------9分
由余弦定理,得cosC= ------------10分
------------10分
∴cosC=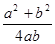 ≥
≥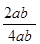 =
=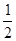 (当且仅当a=b时取等号) ---------------------11分
(当且仅当a=b时取等号) ---------------------11分
∴cosC≥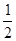 ,
,
∠C是锐角,又∵余弦函数在(0,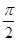 )上递减,∴0<C≤
)上递减,∴0<C≤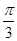
【解析】略

练习册系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|