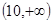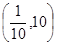题目内容
设定义在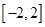 上的奇函数
上的奇函数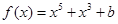
(1).求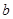 值;(4分)
值;(4分)
(2).若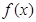 在
在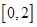 上单调递增,且
上单调递增,且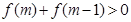 ,求实数
,求实数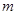 的取值范围.(6分)
的取值范围.(6分)
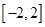 上的奇函数
上的奇函数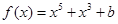
(1).求
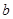 值;(4分)
值;(4分)(2).若
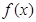 在
在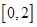 上单调递增,且
上单调递增,且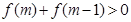 ,求实数
,求实数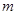 的取值范围.(6分)
的取值范围.(6分)(1)0;(2) .
.
 .
.试题分析:(1)因为
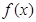 是奇函数,且在
是奇函数,且在 处有意义,所以
处有意义,所以 ,即可求得
,即可求得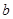 的值;
的值;(2)因为
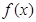 是奇函数,得到
是奇函数,得到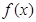 在
在 是单调递增的,不等式
是单调递增的,不等式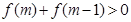 利用函数
利用函数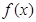 的单调性脱去
的单调性脱去 ,得一不等式,且需要不等式
,得一不等式,且需要不等式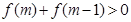 在函数
在函数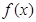 定义域范围内有意义,最后就可求出
定义域范围内有意义,最后就可求出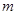 的取值范围.
的取值范围.试题解析:(1)因为函数
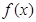 是定义在
是定义在 上的奇函数,所以
上的奇函数,所以 ,解得
,解得 ;
;(2)因为函数
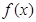 在
在 是增函数,又因为
是增函数,又因为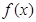 是奇函数,所以
是奇函数,所以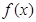 在
在 是单调递增的;
是单调递增的; ,
, ,
,
 ①
①又需要不等式
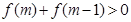 在函数
在函数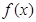 定义域范围内有意义,所以
定义域范围内有意义,所以
 ②
②解①②得
 ,
,所以,
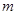 的取值范围为
的取值范围为

练习册系列答案
相关题目
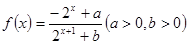 .
.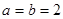 时,证明:函数
时,证明:函数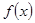 不是奇函数;
不是奇函数;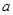 与
与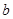 的值;
的值;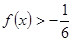 的解集.
的解集.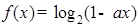 ,在
,在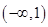 上单调递减,则a的取值范围是 .
上单调递减,则a的取值范围是 .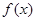 是定义在
是定义在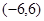 上的偶函数,
上的偶函数,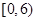 上是单调函数,且
上是单调函数,且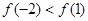 则下列不等式成立的是( )
则下列不等式成立的是( )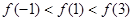

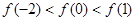
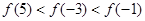
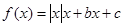 ,给出下列四个命题:
,给出下列四个命题: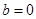 ,
,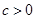 时,
时,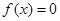 只有一个实数根;
只有一个实数根;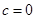 时,
时,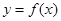 是奇函数;
是奇函数;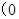 ,
,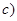 对称;
对称;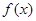 至多有两个零点.
至多有两个零点.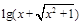 +x,如果f(1-a)+f(1-a2)<0,则a的取值范围是_____
+x,如果f(1-a)+f(1-a2)<0,则a的取值范围是_____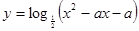 在区间
在区间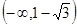 上为增函数,则
上为增函数,则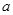 的取值范围是 __________.
的取值范围是 __________.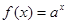 (
( ),数列
),数列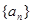 满足
满足 ,
, ,
,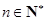 .则
.则 与
与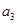 中,较大的是 ;
中,较大的是 ;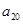 ,
,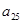 ,
,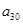 的大小关系是 .
的大小关系是 .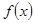 在
在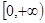 上是增函数,
上是增函数,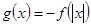 ,若
,若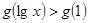 ,则x的取值范围是 ( )
,则x的取值范围是 ( )