Question

已知x²-ax+1=0（x＞0），圆x²+y²=1的圆心到直线y=ax-1的距离的最大值为________．

Answer 1

分析：通过圆心到直线的距离结合已知表达式求出a的最小值，然后求出所求最值．
解答：圆心到直线的距离为：，要使得距离最大，则需a²取得最小值，因为当x＞0时，由x²-ax+1=0（x＞0），
得a=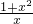=x+≥2，当且仅当x=1时等号成立．即a²的最小值为4，所以所求距离的最大值为：．
故答案为：．
点评：本题考查圆心到直线的距离公式的应用，基本不等式的应用，考查计算能力．