题目内容

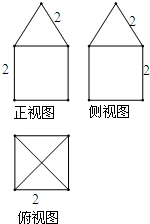（2012•天津模拟）一个几何体的三视图如图所示，则这个几何体表面积为
28
28
．
分析：由三视图可知该几何体为上部是正四棱锥，下部为正方体的组合体．底面边长为2，正四棱锥的斜高为2．分别求出表面积后相加．
解答：解：由三视图可知该几何体为上部是正四棱锥，下部为正方体的组合体．
底面边长为2，正四棱锥的斜高为2
下部正方体的表面积之和为S1=5×2×2=20
上部是正四棱锥侧面积S2=4×
1
2
×2×2=8
所以它的表面积为S1+S2=28
故答案为：28
点评：本题考查三视图求几何体的表面积，考查计算能力，空间想象能力，三视图复原几何体是解题的关键．
练习册系列答案
相关题目
（2012•天津模拟）设y=f（x）在（-∞，1]上有定义，对于给定的实数K，定义fk(x)=
f(x)，f(x)≤K
K，f(x)＞K
，给出函数f（x）=2x+1-4x，若对于任意x∈（-∞，1]，恒有fk（x）=f（x），则（　　）
（2012•天津模拟）已知f（x），g（x）都是定义在R上的函数，且满足以下条件：①f（x）=ax-g（x）（a＞0，且a≠1）；②g（x）≠0；③f（x）•g′（x）＞f′（x）•g（x）．若
f(1)
g(1)
+
f(-1)
g(-1)
=
5
2
，则a等于（　　）
（2012•天津模拟）已知集合M={x|log2x≤1}，N={x|x2-2x≤0}，则“a∈M”是“a∈N”的（　　）
（2012•天津模拟）已知等差数列{an}，a1=2，a3=6，若将a1，a4，a5都加上同一个数，所得的三个数依次成等比数列，则所加的这个数为
-11
-11
．
（2012•天津模拟）如图所示，四棱锥P-ABCD的底面是边长为1的正方形，PA⊥CD，PA=1，PD=
2
，E为PD上一点，PE=2ED．
（Ⅰ）求证：PA⊥平面ABCD；
（Ⅱ）求二面角D-AC-E的余弦值；
（Ⅲ）在侧棱PC上是否存在一点F，使得BF∥平面AEC？若存在，指出F点的位置，并证明；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网