题目内容
已知函数f(x)=lnx-ax+ (a∈R).
(a∈R).
(Ⅰ)当a 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;
(Ⅱ)当a=0时,对于任意的n∈N+,且n≥2,证明:不等式 >
> -
- .
.
(I)解:函数的定义域为(0,+∞),求导函数可得
当a=0时,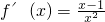 ,令
,令 可得x>1,令
可得x>1,令 ,∵x>0,∴0<x<1,
,∵x>0,∴0<x<1,
∴函数f(x)在(1,+∞)上是增函数,在(0,1)上是减函数;
当a<0时,令 得-ax2+x-1+a>0,解得x>1或x<
得-ax2+x-1+a>0,解得x>1或x< (舍去),此时函数f(x)在(1,+∞_上增函数,在(0,1)上是减函数;
(舍去),此时函数f(x)在(1,+∞_上增函数,在(0,1)上是减函数;
当0<a 时,令
时,令 得-ax2+x-1+a>0,解得
得-ax2+x-1+a>0,解得
此时函数f(x)在(1, )上是增函数,在(0,1)和(
)上是增函数,在(0,1)和( ,+∞)上是减函数 …(6分)
,+∞)上是减函数 …(6分)
(II)证明:由(I)知:a=0时,f(x)=lnx+ -1在(1,+∞)上是增函数,
-1在(1,+∞)上是增函数,
∴x>1时,f(x)>f(1)=0
设g(x)=f(x)-(x2-1)=lnx+ -x2(x>1),则
-x2(x>1),则
∵2x2-2x+1>0恒成立,∴x>1时,g′(x)<0,∴g(x)在(1,+∞)上单调递减
∴x>1时,g(x)<g(1)=0,即f(x)<x2-1
∵f(x)>0,∴ =
= (
( )
)
∴ >
> (1-
(1- +
+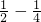 +…+
+…+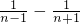 )=
)= =
=
∴不等式得证 …(12分)
分析:(I)确定函数的定义域,求导函数,分类讨论,利用导数的正负,可确定函数的单调性;
(II)先证明x>1时,f(x)>f(1)=0,再设g(x)=f(x)-(x2-1)=lnx+ -x2(x>1),求导函数,确定g(x)在(1,+∞)上单调递减,从而可得
-x2(x>1),求导函数,确定g(x)在(1,+∞)上单调递减,从而可得 =
= (
( ),再叠加,即可得到结论.
),再叠加,即可得到结论.
点评:本题考查导数知识,考查函数的单调性,考查不等式的证明,考查裂项法求和,属于中档题.

当a=0时,
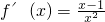 ,令
,令 可得x>1,令
可得x>1,令 ,∵x>0,∴0<x<1,
,∵x>0,∴0<x<1,∴函数f(x)在(1,+∞)上是增函数,在(0,1)上是减函数;
当a<0时,令
 得-ax2+x-1+a>0,解得x>1或x<
得-ax2+x-1+a>0,解得x>1或x< (舍去),此时函数f(x)在(1,+∞_上增函数,在(0,1)上是减函数;
(舍去),此时函数f(x)在(1,+∞_上增函数,在(0,1)上是减函数;当0<a
 时,令
时,令 得-ax2+x-1+a>0,解得
得-ax2+x-1+a>0,解得
此时函数f(x)在(1,
 )上是增函数,在(0,1)和(
)上是增函数,在(0,1)和( ,+∞)上是减函数 …(6分)
,+∞)上是减函数 …(6分)(II)证明:由(I)知:a=0时,f(x)=lnx+
 -1在(1,+∞)上是增函数,
-1在(1,+∞)上是增函数,∴x>1时,f(x)>f(1)=0
设g(x)=f(x)-(x2-1)=lnx+
 -x2(x>1),则
-x2(x>1),则
∵2x2-2x+1>0恒成立,∴x>1时,g′(x)<0,∴g(x)在(1,+∞)上单调递减
∴x>1时,g(x)<g(1)=0,即f(x)<x2-1
∵f(x)>0,∴
 =
= (
( )
)∴
 >
> (1-
(1- +
+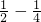 +…+
+…+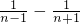 )=
)= =
=
∴不等式得证 …(12分)
分析:(I)确定函数的定义域,求导函数,分类讨论,利用导数的正负,可确定函数的单调性;
(II)先证明x>1时,f(x)>f(1)=0,再设g(x)=f(x)-(x2-1)=lnx+
 -x2(x>1),求导函数,确定g(x)在(1,+∞)上单调递减,从而可得
-x2(x>1),求导函数,确定g(x)在(1,+∞)上单调递减,从而可得 =
= (
( ),再叠加,即可得到结论.
),再叠加,即可得到结论.点评:本题考查导数知识,考查函数的单调性,考查不等式的证明,考查裂项法求和,属于中档题.

练习册系列答案
相关题目