题目内容
已知函数f(x)在定义域(-1,1)上是减函数,且f(1-a)<f(3a-1),则a的取值范围是
(0,
)
| 1 |
| 2 |
(0,
)
.| 1 |
| 2 |
分析:根据已知可将原不等式化为
,解不等式组可得答案.
|
解答:解:∵函数f(x)在定义域(-1,1)上是减函数,
∴不等式f(1-a)<f(3a-1)可化为
解得0<a<
即a的取值范围是(0,
)
故答案为:(0,
)
∴不等式f(1-a)<f(3a-1)可化为
|
解得0<a<
| 1 |
| 2 |
即a的取值范围是(0,
| 1 |
| 2 |
故答案为:(0,
| 1 |
| 2 |
点评:本题考查的知识点是函数的单调性,其中根据函数的定义域和单调性对不等式进行变形是解答的关键,本题易忽略定义为(-1,1)而错解为(-∞,
)
| 1 |
| 2 |

练习册系列答案
相关题目
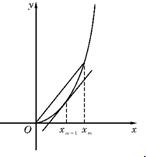 已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
 中ξi的选取是任意的,且In仅于n有关.
中ξi的选取是任意的,且In仅于n有关.