题目内容
甲、乙两人玩猜数字游戏,规则如下:
①连续竞猜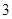 次,每次相互独立;
次,每次相互独立;
②每次竟猜时,先由甲写出一个数字,记为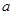 ,再由乙猜测甲写的数字,记为
,再由乙猜测甲写的数字,记为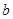 ,已知
,已知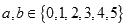 ,若
,若 ,则本次竞猜成功;
,则本次竞猜成功;
③在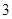 次竞猜中,至少有
次竞猜中,至少有 次竞猜成功,则两人获奖.
次竞猜成功,则两人获奖.
(Ⅰ) 求甲乙两人玩此游戏获奖的概率;
(Ⅱ)现从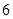 人组成的代表队中选
人组成的代表队中选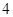 人参加此游戏,这
人参加此游戏,这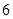 人中有且仅有
人中有且仅有 对双胞胎,记选出的
对双胞胎,记选出的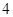 人中含有双胞胎的对数为
人中含有双胞胎的对数为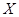 ,求
,求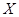 的分布列和期望.
的分布列和期望.
【答案】
(1)
(2)分布列为
|
|
|
|
|
|
|
|
|
|
∴
【解析】
试题分析:解:(Ⅰ)记事件 为甲乙两人一次竞猜成功,则
为甲乙两人一次竞猜成功,则
则甲乙两人获奖的概率为

(Ⅱ)由题意可知6人中选取4人,双胞胎的对数 取值为0,1,2
取值为0,1,2
则 ,
,
 ∴分布列为
∴分布列为
|
|
|
|
|
|
|
|
|
|
∴
考点:古典概型概率和分布列
点评:主要是考查了古典概型概率和分布列的求解,属于基础题。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目







 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,其中
,其中 ,若
,若 ,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( )
,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( )  B.
B. C.
C. D.
D.