题目内容
【题目】已知数列{an}满足a1+2a2+3a3+…+nan=n(n∈N*).
(1)求数列{an}的通项公式an;
(2)令 ![]() ,写出Tn关于n的表达式,并求满足Tn>
,写出Tn关于n的表达式,并求满足Tn> ![]() 时n的取值范围.
时n的取值范围.
【答案】
(1)解:由a1+2a2+3a3+…+nan=n,
可得a1+2a2+3a3+…+(n﹣1)an﹣1=n﹣1(n>1),
相减可得nan=1,即有an= ![]() ,(n>1),
,(n>1),
当n=1时,a1=1,上式也成立,
可得an= ![]() ,(n∈N*);
,(n∈N*);
(2)解:由 ![]() ,
,
结合(1)可得,bn=(2n﹣1)( ![]() )n,
)n,
前n项和Tn=1 ![]() +3(
+3( ![]() )2+…+(2n﹣3)(
)2+…+(2n﹣3)( ![]() )n﹣1+(2n﹣1)(
)n﹣1+(2n﹣1)( ![]() )n,
)n,
![]() Tn=1(
Tn=1( ![]() )2+3(
)2+3( ![]() )3+…+(2n﹣3)(
)3+…+(2n﹣3)( ![]() )n+(2n﹣1)(
)n+(2n﹣1)( ![]() )n+1,
)n+1,
相减可得, ![]() Tn=
Tn= ![]() +2[(
+2[( ![]() )2+…+(
)2+…+( ![]() )n﹣1+(
)n﹣1+( ![]() )n]﹣(2n﹣1)(
)n]﹣(2n﹣1)( ![]() )n+1
)n+1
= ![]() +2
+2  ﹣(2n﹣1)(
﹣(2n﹣1)( ![]() )n+1,
)n+1,
化简可得,前n项和Tn=3﹣ ![]() .
.
由Tn﹣Tn﹣1=3﹣ ![]() ﹣(3﹣
﹣(3﹣ ![]() )=
)= ![]() ,
,
当n≥2时,Tn>Tn﹣1,可得数列{Tn}递增,
由T4=3﹣ ![]() =
= ![]() <
< ![]() ;T5=3﹣
;T5=3﹣ ![]() =
= ![]() >
> ![]() .
.
即有n≥5时,Tn≥T5> ![]() .
.
故n的取值范围是n≥5,且n∈N*
【解析】(1)由条件,可将n换为n﹣1,相减,即可得到所求通项公式;(2)求得bn=(2n﹣1)( ![]() )n , 由数列的求和方法:错位相减法,运用等比数列的求和公式,计算可得Tn , 判断单调性,求得T4 , T5 , 即可得到所求n的范围.
)n , 由数列的求和方法:错位相减法,运用等比数列的求和公式,计算可得Tn , 判断单调性,求得T4 , T5 , 即可得到所求n的范围.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系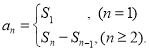 ).
).

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目