题目内容
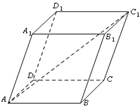
如图所示:一块矩形的太阳能吸光板安装在三棱锥形状的支撑架上,矩形EFGH的四个顶点分别在边AB、BC、CD、AD上,已知AC=a,BD=b,问E、F、G、H在什么位置时吸光板的吸光量最大?
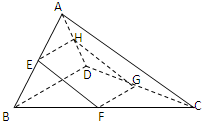

由题意可得 EH∥FG∥BD,EF∥GH∥AC.∵AC=a,BD=b,设
=x,则
=1-x,0<x<1.
由三角形相似可得 EH=x•BD,EF=(1-x)•AC.
故矩形EFGH的面积为 EH•EF=x(1-x)ab,∴当x=
时,矩形EFGH的面积最大,此时矩形吸光板的吸光量最大.
故E、F、G、H在三棱锥的对应边的中点位置时,矩形吸光板的吸光量最大.
| AE |
| AB |
| BE |
| AB |
由三角形相似可得 EH=x•BD,EF=(1-x)•AC.
故矩形EFGH的面积为 EH•EF=x(1-x)ab,∴当x=
| 1 |
| 2 |
故E、F、G、H在三棱锥的对应边的中点位置时,矩形吸光板的吸光量最大.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 是球心
是球心 的半径
的半径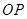 上的两点,且
上的两点,且 ,分别过
,分别过 作垂线于
作垂线于 B、
B、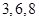 C、
C、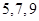 D、
D、

 的圆,且这个几何体是实心球体的一部分,则这个几何体的表面积为 .
的圆,且这个几何体是实心球体的一部分,则这个几何体的表面积为 .

